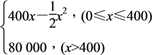题目内容
【题目】已知函数f(x)＝
ax3－bx2＋(2－b)x＋1在x＝x1处取得极大值，在x＝x2处取得极小值，且0＜x1＜1＜x2＜2.
(1)证明：a＞0；
(2)若z＝a＋2b，求z的取值范围.
【答案】见解析
【解析】
(1)证明 求函数f(x)的导数
f′(x)＝ax2－2bx＋2－b.
由函数f(x)在x＝x1处取得极大值，
在x＝x2处取得极小值，
知x1、x2是f′(x)＝0的两个根，
所以f′(x)＝a(x－x1)(x－x2).
当x＜x1时，f(x)为增函数，f′(x)＞0，
由x－x1＜0，x－x2＜0得a＞0.
(2)解 在题设下，0＜x1＜1＜x2＜2等价于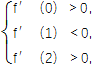
即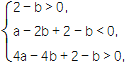
化简得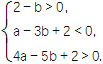
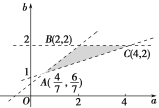
此不等式组表示的区域为平面aOb上的三条直线：
2－b＝0，a－3b＋2＝0，4a－5b＋2＝0所围成的△ABC的内部，其三个顶点分别为A
，B(2，2)，C(4，2).
z在这三点的值依次为
，6，8.
所以z的取值范围为
.
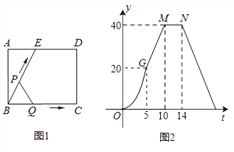
【题目】随着人口老龄化的到来，我国的劳动力人口在不断减少，“延迟退休”已经成为人们越来越关心的话题，为了解公众对“延迟退休”的态度，某校课外研究性学习小组在某社区随机抽取了50人进行调查，将调查情况进行整理后制成下表：
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在
，
的被调查者中赞成“延迟退休”的人数分别是3人和2人，现从这两组的被调查者中各随机选取2人，进行跟踪调查．
（Ⅰ）求年龄在
的被调查者中选取的2人都赞成“延迟退休”的概率；
（Ⅱ）若选中的4人中，不赞成“延迟退休”的人数为
，求随机变量的分布列和数学期望．
【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
（Ⅰ）计算上线考生中抽取的男生成绩的方差
；（结果精确到小数点后一位）
（Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.
