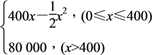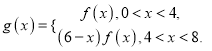题目内容
【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
【答案】(1)![]() (
(![]() 且
且![]() 为正整数);(2)当售价定为每件
为正整数);(2)当售价定为每件![]() 或
或![]() 元,每个月的利润最大,最大的月利润是
元,每个月的利润最大,最大的月利润是![]() 元.
元.
【解析】试题分析:(1)首先计算每一件的利润=售价-成本=![]() ,每月生产
,每月生产![]() 件,然后相乘就是
件,然后相乘就是![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)将函数整理为关于![]() 的二次函数,并且配方,根据定义域求函数的最大值,主要定义域.
的二次函数,并且配方,根据定义域求函数的最大值,主要定义域.
试题解析:解:(1)依题意可得每件商品的售价上涨![]() 元(
元(![]() 为正整数),
为正整数),
则每件商品对应的利润为![]() 元,而对应的销售量为
元,而对应的销售量为![]() ,
,
所以每个月的销售利润为![]() ,其中
,其中![]() 为正整数且
为正整数且![]() .
.
(2)由![]()
可得利润![]() 是关于
是关于![]() 的一元二次函数
的一元二次函数
开口向下且对称轴为![]() ,所以当
,所以当![]() 取
取![]() 时,
时,
即每件商品的售价定为![]() 元或
元或![]() 元时,每个月的利润最大,最大利润为
元时,每个月的利润最大,最大利润为![]() 元
元

练习册系列答案
相关题目
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.