题目内容
【题目】双曲线C的方程为![]() 离心率
离心率![]() 顶点到渐近线的距离为
顶点到渐近线的距离为![]()
(1)求双曲线C的方程;
(2)点P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一,二象限.若![]() 求△AOB面积的取值范围。
求△AOB面积的取值范围。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)先由双曲线标准方程求得顶点坐标和渐近线方程,进而根据顶点到渐近线的距离求得a,b和c的关系,进而根据离心率求得a和c的关系,最后根据c=![]() 综合得方程组求得a,b和c,则双曲线方程可得.(Ⅱ)由(Ⅰ)可求得渐近线方程,设A(m,2m),B(-n,2n),根据
综合得方程组求得a,b和c,则双曲线方程可得.(Ⅱ)由(Ⅰ)可求得渐近线方程,设A(m,2m),B(-n,2n),根据![]() 得P点的坐标代入双曲线方程化简整理m,n与λ的关系式,设∠AOB=2θ,进而根据直线的斜率求得tanθ,进而求得sin2θ,进而表示出|OA|,得到△AOB的面积的表达式,根据λ的范围求得三角形面积的最大值和最小值,△AOB面积的取值范围可得
得P点的坐标代入双曲线方程化简整理m,n与λ的关系式,设∠AOB=2θ,进而根据直线的斜率求得tanθ,进而求得sin2θ,进而表示出|OA|,得到△AOB的面积的表达式,根据λ的范围求得三角形面积的最大值和最小值,△AOB面积的取值范围可得
试题解析:(Ⅰ)由题意知,双曲线C的顶点![]() 到渐近线
到渐近线![]()
∴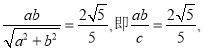 [由
[由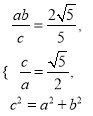 得
得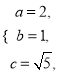 ∴双曲线C的方程为
∴双曲线C的方程为![]()
(Ⅱ)设直线AB的方程为![]() 由题意知
由题意知![]() 由{
由{![]()
得A点的坐标为![]() 由{
由{![]() 得B点的坐标为
得B点的坐标为![]()
由![]() 得P点的坐标为
得P点的坐标为![]()
将P点坐标代入![]() 设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).
![]() =
=![]()
设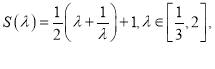 在
在![]() 上是减函数,在
上是减函数,在![]() 上是减函数
上是减函数
当![]() 时,△AOB的面积取得最小值2,当
时,△AOB的面积取得最小值2,当![]() 时,△AOB的面积取得最大值
时,△AOB的面积取得最大值![]()
∴△AOB面积的取值范围是![]()

练习册系列答案
相关题目