Question

【题目】如图所示，在所有棱长都为的三棱柱中，侧棱，点为棱的中点．

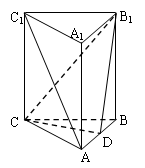
（1）求证：∥平面；

（2）求四棱锥的体积．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：本题主要考查线线平行、线面平行、线线垂直、线面垂直、四棱锥的体积等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力．第一问，作出辅助线，根据是的中位线，得∥，再根据线面平行的判定，得∥平面；由为正三角形，得，而平面，可转化为平面，则利用线面垂直的性质，得，利用线面垂直的判定得平面，则可以判断是四棱锥的高，最后利用四棱锥的体积公式计算即可．

试题解析：（1）连结，设与交于点，

则点是的中点，连结，

因为点为的中点，

所以是的中位线，

所以∥，

因为平面，面，

所以∥平面．

（2）取线段中点，连结，

，点为线段中点，

．

又平面

即平面，平面

，

，

平面，则是四棱锥的高

．