题目内容
已知函数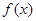 是定义在R上的奇函数,当
是定义在R上的奇函数,当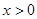 时,
时,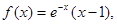 给出以下命题:
给出以下命题:
①当x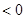 时,
时,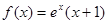 ;
;
②函数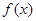 有五个零点;
有五个零点;
③若关于 的方程
的方程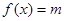 有解,则实数
有解,则实数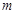 的取值范围是
的取值范围是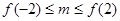 ;
;
④对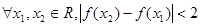 恒成立.其中,正确结论的代号是 .
恒成立.其中,正确结论的代号是 .
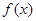 是定义在R上的奇函数,当
是定义在R上的奇函数,当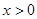 时,
时,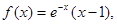 给出以下命题:
给出以下命题:①当x
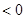 时,
时,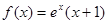 ;
; ②函数
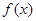 有五个零点;
有五个零点;③若关于
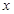 的方程
的方程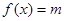 有解,则实数
有解,则实数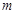 的取值范围是
的取值范围是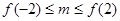 ;
;④对
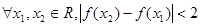 恒成立.其中,正确结论的代号是 .
恒成立.其中,正确结论的代号是 . ①④
①当x<0,所以-x>0,所以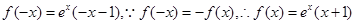 .正确;
.正确;
②当x>0时,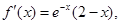 所以
所以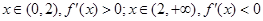 ,因为1>f(2)=
,因为1>f(2)=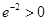 ,所以当x>0时,f(x)的图像与x轴有1个交点,由于f(x)是奇函数,所以x<0时,f(x)的图像与x轴有1个交点,又因为f(0)=0,所以函数
,所以当x>0时,f(x)的图像与x轴有1个交点,由于f(x)是奇函数,所以x<0时,f(x)的图像与x轴有1个交点,又因为f(0)=0,所以函数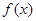 有3个零点.
有3个零点.
③在②的基础上,画出函数f(x)的图像,从图像可看出f(x)=m恒有解.并且范围应为-1<m<1.因而此项错;④从图像可看出④是正确的.
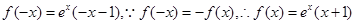 .正确;
.正确;②当x>0时,
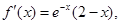 所以
所以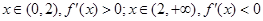 ,因为1>f(2)=
,因为1>f(2)=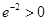 ,所以当x>0时,f(x)的图像与x轴有1个交点,由于f(x)是奇函数,所以x<0时,f(x)的图像与x轴有1个交点,又因为f(0)=0,所以函数
,所以当x>0时,f(x)的图像与x轴有1个交点,由于f(x)是奇函数,所以x<0时,f(x)的图像与x轴有1个交点,又因为f(0)=0,所以函数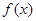 有3个零点.
有3个零点.③在②的基础上,画出函数f(x)的图像,从图像可看出f(x)=m恒有解.并且范围应为-1<m<1.因而此项错;④从图像可看出④是正确的.

练习册系列答案
相关题目
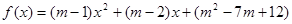 为偶函数,则
为偶函数,则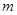 =( )
=( )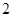
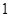
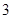
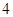
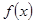 是定义在
是定义在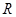 上的奇函数,当
上的奇函数,当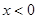 时,
时,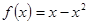 ,则当
,则当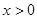 时,
时,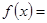 ( )
( )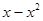
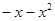
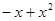
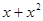
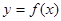
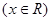 满足
满足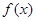 是偶函数,又
是偶函数,又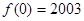 ,
,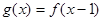 为奇函数,则
为奇函数,则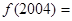 _______
_______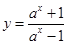 ②
②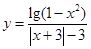 ③
③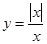 ④
④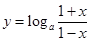
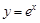
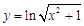
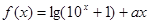 是偶函数,
是偶函数,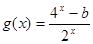 是奇函数,那么
是奇函数,那么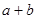 的值为( )
的值为( )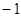

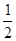
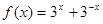 与
与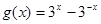 的定义域均为R,则
的定义域均为R,则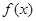 与
与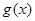 与均为偶函数 B.
与均为偶函数 B.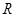 上的偶函数
上的偶函数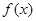 满足
满足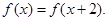 当
当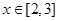 时,
时,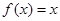 ,则
,则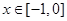 时,
时,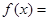 ________.
________.