题目内容
函数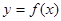
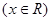 满足
满足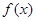 是偶函数,又
是偶函数,又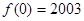 ,
,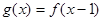 为奇函数,则
为奇函数,则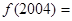 _______
_______
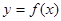
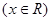 满足
满足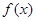 是偶函数,又
是偶函数,又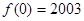 ,
,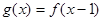 为奇函数,则
为奇函数,则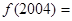 _______
_______2003
g(x)=f(x-1)为奇函数,所以 g(-x)=-g(x) 即 f(-x-1)=-f(x-1),又因为f(x)为偶函数,所以 f(x)=f(-x),所以 f(x+2)="f(-x-2)=f[-(x+1)-1]=-f(x+1-1)=-f(x)," f(x+4)=-f(x+2)=f(x).
所以f(x)是以4为一个周期的周期函数,故 f(2004)=f(0)=2003.
所以f(x)是以4为一个周期的周期函数,故 f(2004)=f(0)=2003.

练习册系列答案
相关题目
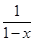 的图象与函数y=2sinπx(-2≤x≤4)的图象所有交点的横坐标之
的图象与函数y=2sinπx(-2≤x≤4)的图象所有交点的横坐标之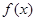 是定义在
是定义在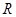 上的偶函数,且
上的偶函数,且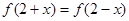 ,当
,当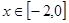 时,
时,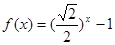 ,若在区间
,若在区间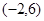 内关于
内关于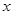 的方程
的方程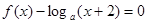 ,恰有
,恰有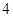 个不同的实数根,则实数
个不同的实数根,则实数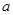
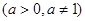 的取值范围是
的取值范围是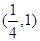
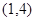
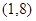
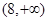
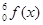 dx=8,则∫
dx=8,则∫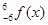 dx等于 ( )
dx等于 ( ) 
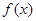 是定义在R上的奇函数,当
是定义在R上的奇函数,当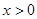 时,
时,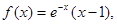 给出以下命题:
给出以下命题: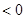 时,
时,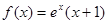 ;
; 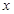 的方程
的方程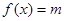 有解,则实数
有解,则实数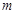 的取值范围是
的取值范围是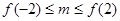 ;
;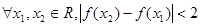 恒成立.其中,正确结论的代号是 .
恒成立.其中,正确结论的代号是 . 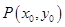 是函数
是函数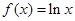 图象上一点,过点
图象上一点,过点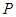 的切线与
的切线与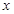 轴交于
轴交于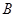 ,过点
,过点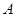 .
.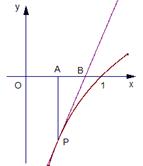
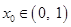 ,求
,求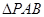 的面积
的面积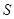 的最大值,并求此时
的最大值,并求此时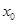 的值.
的值.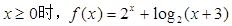 则f (-1)=
则f (-1)= 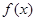 满足
满足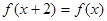 ,且当
,且当 时,
时, 的值为 。
的值为 。