Question

【题目】已知定义域为R的函数f（x）= 是奇函数．
（Ⅰ）求a，b的值；
（Ⅱ）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求k的取值范围．

Answer 1

【答案】解：（Ⅰ）因为f（x）是奇函数，所以f（0）=0，
即
又由f（1）=﹣f（﹣1）知 ．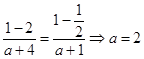
所以a=2，b=1．
经检验a=2，b=1时， 是奇函数．
（Ⅱ）由（Ⅰ）知 ，
易知f（x）在（﹣∞，+∞）上为减函数．
又因为f（x）是奇函数，
所以f（t2﹣2t）+f（2t2﹣k）＜0
等价于f（t2﹣2t）＜﹣f（2t2﹣k）=f（k﹣2t2），
因为f（x）为减函数，由上式可得：t2﹣2t＞k﹣2t2 ．
即对一切t∈R有：3t2﹣2t﹣k＞0，
从而判别式 ．
所以k的取值范围是k＜﹣
【解析】（Ⅰ）利用奇函数定义，在f（﹣x）=﹣f（x）中的运用特殊值求a，b的值；
（Ⅱ）首先确定函数f（x）的单调性，然后结合奇函数的性质把不等式f（t2﹣2t）+f（2t2﹣k）＜0转化为关于t的一元二次不等式，最后由一元二次不等式知识求出k的取值范围．
【考点精析】本题主要考查了函数的奇函数的相关知识点，需要掌握一般地，对于函数f(x)的定义域内的任意一个x，都有f(－x)=—f(x)，那么f(x)就叫做奇函数才能正确解答此题．