题目内容
4.求y=$\sqrt{3-x}$-$\sqrt{x}$-1的最值.分析 求得定义域为[0,3],再由函数单调性的性质判断函数在定义域上的单调性,即可得到最值.
解答 解:y=$\sqrt{3-x}$-$\sqrt{x}$-1的定义域为[0,3],
由y=-$\sqrt{x}$在[0,3]递减,
y=$\sqrt{3-x}$在[0,3]递减,
则函数y=$\sqrt{3-x}$-$\sqrt{x}$-1在[0,3]递减,
由x=0时,y=$\sqrt{3}$-1;
x=3时,y=-$\sqrt{3}$-1,
故函数的最小值为-$\sqrt{3}$-1,最大值为$\sqrt{3}$-1.
点评 本题考查函数的最值的求法,主要考查根式函数的单调性的运用,属于中档题.

练习册系列答案
相关题目
 :若
:若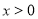 ,则函数
,则函数 的最小值为
的最小值为 ;命题
;命题 :若
:若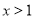 ,则
,则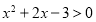 .则下列命题是真命题的是( )
.则下列命题是真命题的是( ) B.
B.
 D.
D.