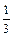题目内容
(本小题满分14分) 
设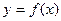 是定义在
是定义在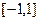 上的偶函数,又
上的偶函数,又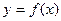 的图象与函数
的图象与函数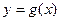 的图象关于直线
的图象关于直线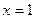 对称,且当
对称,且当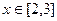 时,
时,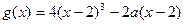 .
.
(1)求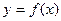 的表达式;
的表达式;
(2)是否存在正实数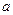 ,使
,使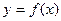 的图象最低点在直线
的图象最低点在直线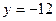 上?若存在,求出
上?若存在,求出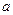 ;若不存在,说明理由.
;若不存在,说明理由.

设
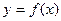 是定义在
是定义在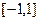 上的偶函数,又
上的偶函数,又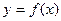 的图象与函数
的图象与函数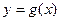 的图象关于直线
的图象关于直线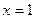 对称,且当
对称,且当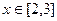 时,
时,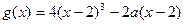 .
.(1)求
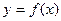 的表达式;
的表达式;(2)是否存在正实数
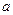 ,使
,使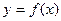 的图象最低点在直线
的图象最低点在直线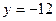 上?若存在,求出
上?若存在,求出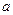 ;若不存在,说明理由.
;若不存在,说明理由.(1)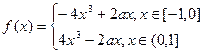
(2)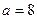 使
使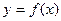 的图象最低点在直线
的图象最低点在直线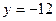 上.
上.
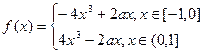
(2)
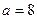 使
使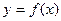 的图象最低点在直线
的图象最低点在直线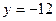 上.
上.(1)当 时,
时,
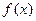 上的
上的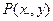 关于直线
关于直线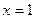 对称的点为
对称的点为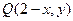 , …………………2分
, …………………2分
此时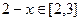 ,代入
,代入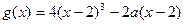 ,
,
得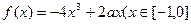 ………………………………5分
………………………………5分

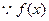 在
在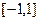 上是偶函数,
上是偶函数,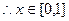 时,
时,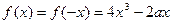
即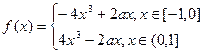 ……………………………6分
……………………………6分
(2)命题转化为:是否存在正实数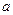 ,使
,使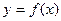 的最小值是
的最小值是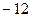 .
.
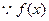 在
在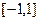 上是偶函数,只要考虑
上是偶函数,只要考虑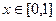 即可. ………………………………8分
即可. ………………………………8分
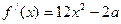 ,令
,令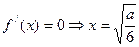 . ………………………………9分
. ………………………………9分
(i)当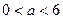 时,
时,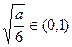 ,且
,且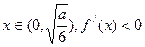 ,
,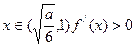 ,
,
由此可知,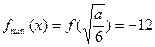 ,
,
解得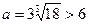 ,矛盾. ………………………………11分
,矛盾. ………………………………11分
(ii)当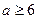 时,
时,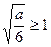 ,此时
,此时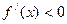 ,
,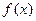 是[0,1]上减函数,
是[0,1]上减函数,
所以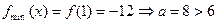 ………………………………13分
………………………………13分
综上可知,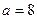 使
使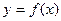 的图象最低点在直线
的图象最低点在直线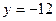 上. …………………14分
上. …………………14分
 时,
时,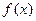 上的
上的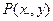 关于直线
关于直线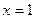 对称的点为
对称的点为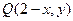 , …………………2分
, …………………2分此时
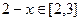 ,代入
,代入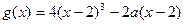 ,
,得
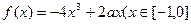 ………………………………5分
………………………………5分
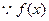 在
在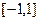 上是偶函数,
上是偶函数,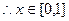 时,
时,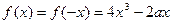
即
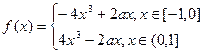 ……………………………6分
……………………………6分(2)命题转化为:是否存在正实数
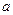 ,使
,使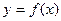 的最小值是
的最小值是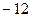 .
. 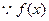 在
在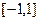 上是偶函数,只要考虑
上是偶函数,只要考虑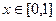 即可. ………………………………8分
即可. ………………………………8分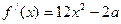 ,令
,令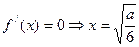 . ………………………………9分
. ………………………………9分(i)当
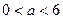 时,
时,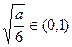 ,且
,且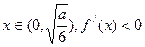 ,
,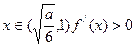 ,
,由此可知,
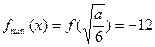 ,
, 解得
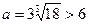 ,矛盾. ………………………………11分
,矛盾. ………………………………11分(ii)当
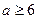 时,
时,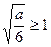 ,此时
,此时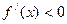 ,
,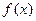 是[0,1]上减函数,
是[0,1]上减函数,所以
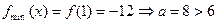 ………………………………13分
………………………………13分综上可知,
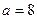 使
使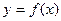 的图象最低点在直线
的图象最低点在直线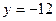 上. …………………14分
上. …………………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
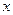 ,且
,且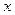
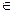 (0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.
(0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.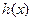 ;
;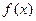 的定义域为R,对任意的
的定义域为R,对任意的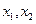 都满足。
都满足。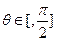 时,不等式
时,不等式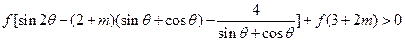
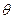 恒成立,如存在,求出m的取值范围;若不存在,说明理由。
恒成立,如存在,求出m的取值范围;若不存在,说明理由。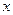 的方程
的方程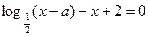 的根在
的根在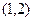 内,则实数
内,则实数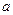 的取值范围是( )
的取值范围是( )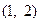
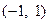
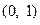
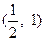
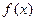 和偶函数
和偶函数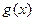 满足
满足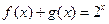 ,若不等式
,若不等式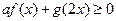 对
对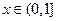 恒成立,则实数
恒成立,则实数 的取值范围是 。
的取值范围是 。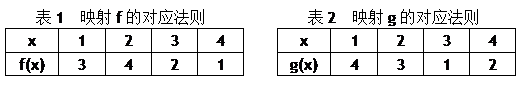
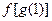 相同的是
相同的是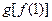
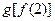
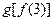
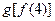
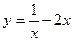 的图像关于 ( )
的图像关于 ( )
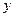 轴对称
轴对称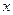 轴对称
轴对称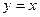 对称
对称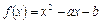 的两个零点是2和3,则函数
的两个零点是2和3,则函数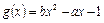 的零点是( )
的零点是( )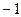 和
和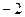
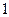 和
和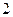
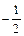 和
和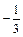
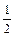 和
和