题目内容
(本小题满分12分)已知函数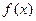 的定义域为R,对任意的
的定义域为R,对任意的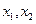 都满足。
都满足。
(I)判断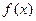 的单调性和奇偶性;
的单调性和奇偶性;
(II)是否存在这样的实数m,当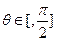 时,不等式
时,不等式
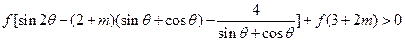
对所有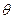 恒成立,如存在,求出m的取值范围;若不存在,说明理由。
恒成立,如存在,求出m的取值范围;若不存在,说明理由。
 的定义域为R,对任意的
的定义域为R,对任意的 都满足。
都满足。(I)判断
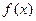 的单调性和奇偶性;
的单调性和奇偶性;(II)是否存在这样的实数m,当
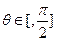 时,不等式
时,不等式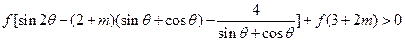
对所有
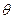 恒成立,如存在,求出m的取值范围;若不存在,说明理由。
恒成立,如存在,求出m的取值范围;若不存在,说明理由。(I)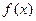 是奇函数,在
是奇函数,在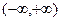 上是增函数;
上是增函数;
(II)存在,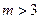
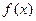 是奇函数,在
是奇函数,在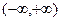 上是增函数;
上是增函数;(II)存在,
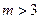
(I)令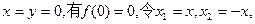
有
即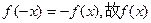 为奇函数。 ………………2分
为奇函数。 ………………2分
在R上任取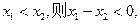
由题意知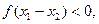
则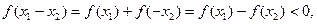
故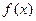 是增函数 ………………6分
是增函数 ………………6分
(II)要使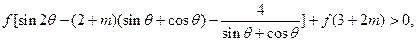
只须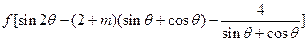
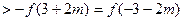
又由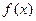 为单调增函数有
为单调增函数有
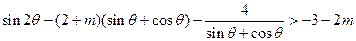 …………8分
…………8分
令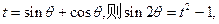
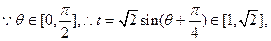
原命题等价于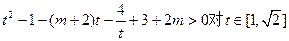 恒成立。…………10分
恒成立。…………10分
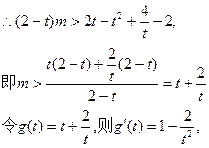
当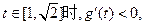
故 上为减函数,
上为减函数,
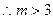 时,原命题成立。 ………………12分
时,原命题成立。 ………………12分
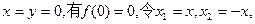
有

即
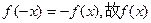 为奇函数。 ………………2分
为奇函数。 ………………2分在R上任取
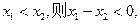
由题意知
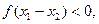
则
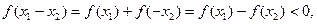
故
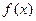 是增函数 ………………6分
是增函数 ………………6分(II)要使
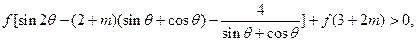
只须
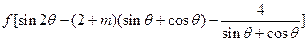
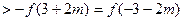
又由
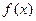 为单调增函数有
为单调增函数有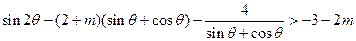 …………8分
…………8分令
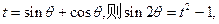
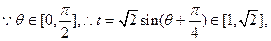
原命题等价于
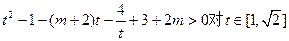 恒成立。…………10分
恒成立。…………10分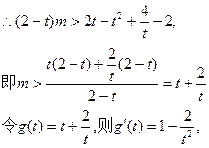
当
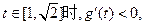
故
 上为减函数,
上为减函数,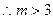 时,原命题成立。 ………………12分
时,原命题成立。 ………………12分
练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目

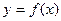 是定义在
是定义在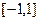 上的偶函数,又
上的偶函数,又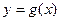 的图象关于直线
的图象关于直线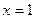 对称,且当
对称,且当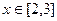 时,
时,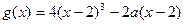 .
.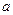 ,使
,使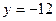 上?若存在,求出
上?若存在,求出
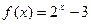 零点所在的区间是 ( )
零点所在的区间是 ( )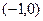
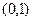
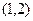
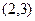
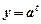 (t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于
(t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于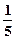 ;②每月减少的有害物质量都相等;③若剩留量为
;②每月减少的有害物质量都相等;③若剩留量为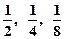 所经过的时间分别是
所经过的时间分别是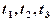 ,则
,则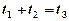 . 其中所有正确的叙述是
. 其中所有正确的叙述是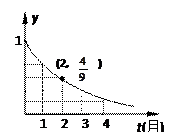
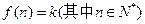 ,k是
,k是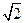 的小数点后第n位数,
的小数点后第n位数,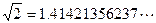 ,
,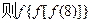 的值等于( )
的值等于( )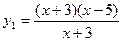 ,
,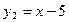 ;
;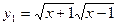 ,
,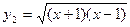 ;
;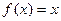 ,
,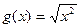 ;
;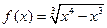 ,
,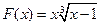 ;
;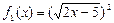 ,
,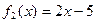 。
。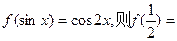 ( )
( )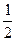
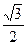
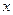 的方程
的方程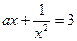 正实数解有且仅有一个,那么实数
正实数解有且仅有一个,那么实数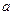 的取值范围为( )
的取值范围为( )