题目内容
20.设a=tan$\frac{3}{4}$π,b=cos$\frac{π}{4}$,c=(1+sin$\frac{6}{5}$π)0,则a,b,c的大小关系是( )| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
分析 由题意可求出a、b、c的值,比较可得大小.
解答 解:由题意可得a=tan$\frac{3}{4}$π=tan(π-$\frac{π}{4}$)=-tan$\frac{π}{4}$=-1;
b=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,c=(1+sin$\frac{6}{5}$π)0=1,
∴c>b>a,
故选:A.
点评 本题考查特殊角的三角函数值的大小比较,属基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
11.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(89)+f(90)为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
5.已知平面向量$\vec a,\vec b,\vec c$满足:$\vec a$⊥$\vec c$,$\vec b•\vec c$=-2,|${\vec c}$|=2,$\vec c$=$\vec a$+λ$\vec b$,则实数λ的值为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
9.若f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,则f(2x)等于( )
| A. | 2f(x) | B. | 2[f(x)+g(x)] | C. | 2g(x) | D. | 2f(x)•g(x) |
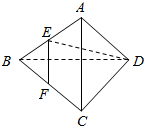 如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.
如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.