题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{2+|x-2|,}&{x≥0}\\{{x}^{2}}&{x<0}\end{array}\right.$,当函数g(x)=k-f(x)有三个零点时,实数k的取值范围是( )| A. | <k<2 | B. | k≥2 | C. | 2<k≤4 | D. | 2≤k≤4 |
分析 根据函数和方程之间的关系转化为y=k与y=f(x)有三个交点,利用数形结合进行求解即可.
解答 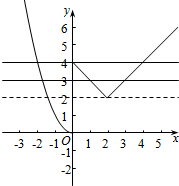 解:由g(x)=k-f(x)=0得k=f(x),即方程k=f(x)有3个根,
解:由g(x)=k-f(x)=0得k=f(x),即方程k=f(x)有3个根,
则等价为y=k与y=f(x)有三个交点,
作出f(x)的图象如图:
要使y=k与y=f(x)有三个交点,
则2<k≤4,
故选:C.
点评 本题主要考查函数与方程的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
20.设a=tan$\frac{3}{4}$π,b=cos$\frac{π}{4}$,c=(1+sin$\frac{6}{5}$π)0,则a,b,c的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
15.若椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的离心率为$\frac{1}{2}$,则双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{3}}}{2}x$ | B. | $y=±\frac{{2\sqrt{3}}}{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | y=±x |
20.函数y=$\frac{x+2}{x-1}$(x≠1)在区间[2,5)上的最大值、最小值分别是( )
| A. | $\frac{7}{4}$,4 | B. | 无最大值,最小值7 | ||
| C. | 4,0 | D. | 最大值4,无最小值 |
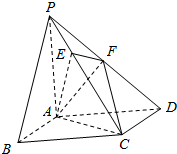 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.