题目内容
双曲线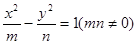 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线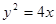 的焦点重
的焦点重
合,则mn的值为 ( )
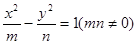 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线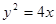 的焦点重
的焦点重合,则mn的值为 ( )
A.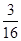 | B.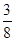 | C.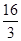 | D.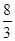 |
A.
抛物线
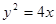 的焦点为
的焦点为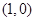 ,双曲线
,双曲线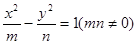 有一个焦点与抛物线
有一个焦点与抛物线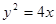 的焦点重合,所以
的焦点重合,所以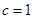 ,离心率为2,
,离心率为2,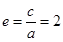 ,则
,则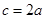 ,
,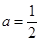 ,
,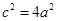 ,
,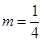 ,
,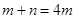 ,
,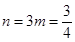 ,
,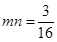 ,故选择A
,故选择A
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
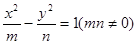 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线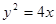 的焦点重
的焦点重A.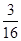 | B.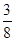 | C.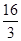 | D.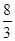 |
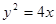 的焦点为
的焦点为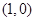 ,双曲线
,双曲线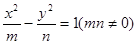 有一个焦点与抛物线
有一个焦点与抛物线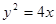 的焦点重合,所以
的焦点重合,所以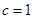 ,离心率为2,
,离心率为2,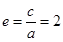 ,则
,则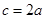 ,
,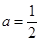 ,
,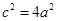 ,
,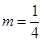 ,
,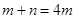 ,
,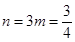 ,
,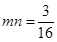 ,故选择A
,故选择A
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案