题目内容
已知动点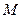 的坐标满足
的坐标满足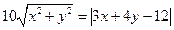 ,则动点
,则动点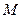 的轨迹是( )
的轨迹是( )
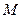 的坐标满足
的坐标满足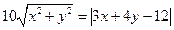 ,则动点
,则动点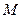 的轨迹是( )
的轨迹是( )| A.椭圆 | B.双曲线 | C.抛物线 | D.以上都不对 |
D
由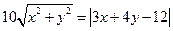 得
得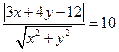 ,∴
,∴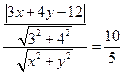 ,即
,即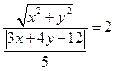 ,这个等式的含义是:
,这个等式的含义是: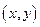 到
到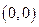 的距离与到直线
的距离与到直线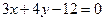 的距离的比是一个定值
的距离的比是一个定值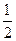 ,这符合椭圆的定义,∴动点
,这符合椭圆的定义,∴动点 的轨迹是椭圆,故选
的轨迹是椭圆,故选 。
。
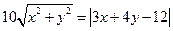 得
得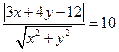 ,∴
,∴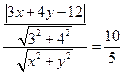 ,即
,即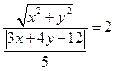 ,这个等式的含义是:
,这个等式的含义是: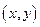 到
到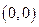 的距离与到直线
的距离与到直线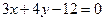 的距离的比是一个定值
的距离的比是一个定值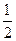 ,这符合椭圆的定义,∴动点
,这符合椭圆的定义,∴动点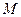 的轨迹是椭圆,故选
的轨迹是椭圆,故选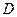 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
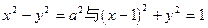
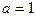
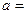 0
0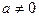
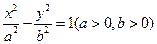 的离心率为
的离心率为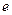 ,右准线
,右准线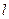 与两渐近线交于P,Q两点,其右焦点为F,且△PQF为等边三角形。
与两渐近线交于P,Q两点,其右焦点为F,且△PQF为等边三角形。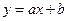 截得弦长为
截得弦长为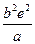 ,求双曲线方程;
,求双曲线方程;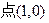 ,以F为左焦点,为
,以F为左焦点,为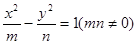 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线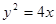 的焦点重
的焦点重
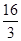
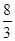
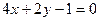 ;②
;② 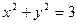 ;③
;③ 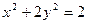 ;
;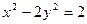 .其中与直线2 x + y +3=0有交点的所有曲线是
.其中与直线2 x + y +3=0有交点的所有曲线是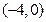 ,
,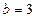 ,其焦点在
,其焦点在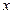 轴上,则该椭圆的标准方程为 。
轴上,则该椭圆的标准方程为 。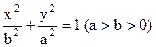 ,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
,求与这个椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形面积最大,并求相应的四边形的顶点坐标
 ,y
,y )、B(x
)、B(x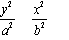 (a > b > 0) 上的两点,
(a > b > 0) 上的两点,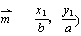 ,
,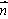 = (
= (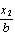 ,
,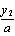 ),且满足
),且满足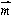 ·
·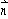 = 0,椭圆的离心率e =
= 0,椭圆的离心率e = 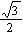 ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.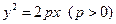 的焦点与双曲线
的焦点与双曲线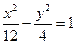 的右焦点重合,则
的右焦点重合,则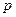 的值为C
的值为C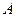 .
. 
 .
. 
 .
. 
 .
.