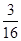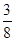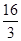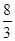题目内容
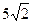

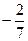
解法一:设所求的椭圆为: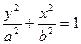
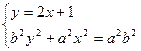
代入化简为: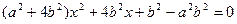
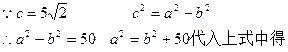
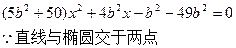

解法二:设直线与椭圆相义于两点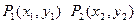

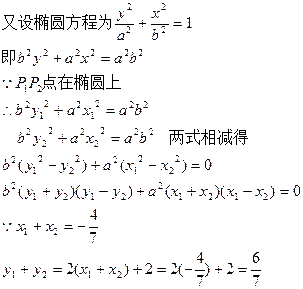
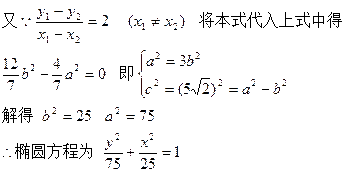
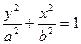
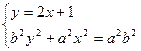
代入化简为:
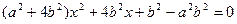
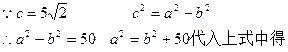
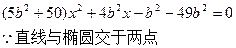

解法二:设直线与椭圆相义于两点
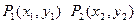

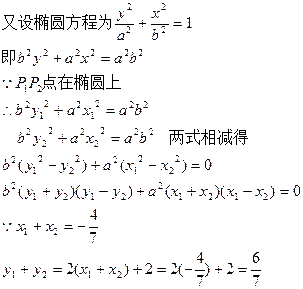
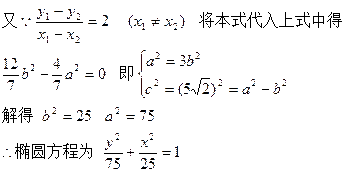
由题设知这是中心在原点,焦点在y轴的椭圆。
直线与椭圆相交所得弦的中点横坐标已知是建立含待定系数a,b的一个方程,另一个是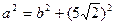 解方程组便可。
解方程组便可。
另外也可以先设出直线与椭圆相交结的端点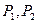 的坐标,由于
的坐标,由于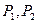 两点在椭圆上,故而坐标满足椭圆方程,然后两式相减,若
两点在椭圆上,故而坐标满足椭圆方程,然后两式相减,若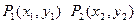 则:
则: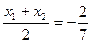
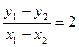 (直线的斜率)也可求出待定系数的值。
(直线的斜率)也可求出待定系数的值。
说明:本题解法一是规范的待定系数法的解法。
解法二是利用曲线与方程的关系,化简得到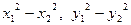 这样两个“平方差”其中一个平方差
这样两个“平方差”其中一个平方差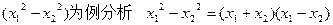 这两个因式表示的分别是弦
这两个因式表示的分别是弦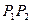 的中点横坐标的2倍,又因直线
的中点横坐标的2倍,又因直线 中斜率为2,因而直线与椭圆交点
中斜率为2,因而直线与椭圆交点 中,
中,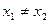 ,为些用
,为些用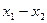 去除等式
去除等式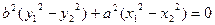 的两边时,便得到
的两边时,便得到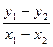 的式子,而这正是直线l的斜率是已知的,为此较容易的得到a,b的一个方程,此法涉及到直线与圆锥曲线相交弦的中点有关问题时(若直线斜率未知也可以用此法求点)使用较简捷。
的式子,而这正是直线l的斜率是已知的,为此较容易的得到a,b的一个方程,此法涉及到直线与圆锥曲线相交弦的中点有关问题时(若直线斜率未知也可以用此法求点)使用较简捷。
直线与椭圆相交所得弦的中点横坐标已知是建立含待定系数a,b的一个方程,另一个是
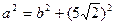 解方程组便可。
解方程组便可。另外也可以先设出直线与椭圆相交结的端点
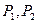 的坐标,由于
的坐标,由于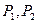 两点在椭圆上,故而坐标满足椭圆方程,然后两式相减,若
两点在椭圆上,故而坐标满足椭圆方程,然后两式相减,若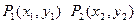 则:
则: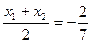
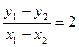 (直线的斜率)也可求出待定系数的值。
(直线的斜率)也可求出待定系数的值。说明:本题解法一是规范的待定系数法的解法。
解法二是利用曲线与方程的关系,化简得到
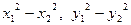 这样两个“平方差”其中一个平方差
这样两个“平方差”其中一个平方差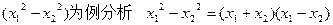 这两个因式表示的分别是弦
这两个因式表示的分别是弦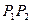 的中点横坐标的2倍,又因直线
的中点横坐标的2倍,又因直线 中斜率为2,因而直线与椭圆交点
中斜率为2,因而直线与椭圆交点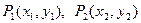 中,
中,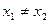 ,为些用
,为些用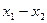 去除等式
去除等式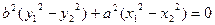 的两边时,便得到
的两边时,便得到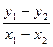 的式子,而这正是直线l的斜率是已知的,为此较容易的得到a,b的一个方程,此法涉及到直线与圆锥曲线相交弦的中点有关问题时(若直线斜率未知也可以用此法求点)使用较简捷。
的式子,而这正是直线l的斜率是已知的,为此较容易的得到a,b的一个方程,此法涉及到直线与圆锥曲线相交弦的中点有关问题时(若直线斜率未知也可以用此法求点)使用较简捷。
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 的半径为
的半径为 的定圆
的定圆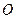 的两互相垂直的直径,作动弦
的两互相垂直的直径,作动弦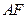 交
交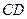 于
于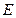 ,引
,引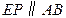 ,且交
,且交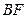 于
于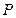 ,求点
,求点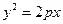 的焦点与双曲线
的焦点与双曲线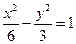 的右焦点重合,则
的右焦点重合,则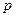 的值为 .
的值为 .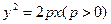 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.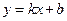 与抛物线C交于两点
与抛物线C交于两点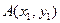 ,
,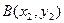 ,且
,且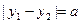 (
(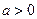 ,且
,且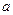 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于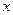 轴的直线交抛物线于点D,连结AD、 BD得到
轴的直线交抛物线于点D,连结AD、 BD得到 .
.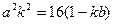 ;
;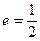
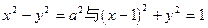
 0
0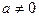
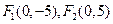 ,点
,点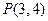 是双曲线的渐近线与椭圆的一个交点,求双曲线与椭圆的方程。
是双曲线的渐近线与椭圆的一个交点,求双曲线与椭圆的方程。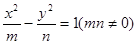 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线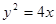 的焦点重
的焦点重