题目内容
【题目】已知数列{an}满足a1=1,a2=2,an+2=(1+cos2 ![]() )an+sin2
)an+sin2 ![]() ,则该数列的前10项和为 .
,则该数列的前10项和为 .
【答案】77
【解析】解:因为a1=1,a2=2,所以a3=(1+cos2 ![]() )a1+sin2
)a1+sin2 ![]() =a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.
=a1+1=2,a4=(1+cos2π)a2+sin2π=2a2=4.
一般地,当n=2k﹣1(k∈N*)时,a2k+1=[1+cos2 ![]() ]a2k﹣1+sin2
]a2k﹣1+sin2 ![]() =a2k﹣1+1,即a2k+1﹣a2k﹣1=1.
=a2k﹣1+1,即a2k+1﹣a2k﹣1=1.
所以数列{a2k﹣1}是首项为1、公差为1的等差数列,因此a2k﹣1=k.
当n=2k(k∈N*)时,a2k+2=(1+cos2 ![]() )a2k+sin2
)a2k+sin2 ![]() =2a2k .
=2a2k .
所以数列{a2k}是首项为2、公比为2的等比数列,因此a2k=2k .
该数列的前10项的和为1+2+2+4+3+8+4+16+5+32=77
所以答案是:77
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系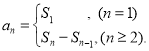 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

