题目内容
10.若函数f(x)=3ax2+(3-4a)x-4的零点总在(0,2)内,则实数a的取值范围是(-∞,-$\frac{1}{2}$)∪{0}.分析 通过讨论a=0和a≠0两种情况,从而综合得到结论.
解答 解:①a=0时,f(x)=3x-4,令f(x)=0,显然x=$\frac{4}{3}$在(0,2)内,成立;
②a≠0时,f(x)=3ax2+(3-4a)x-4=(3x-4)(ax+1),
令f(x)=0,得:x=$\frac{4}{3}$,或x=-$\frac{1}{a}$,
∴只需0<-$\frac{1}{a}$<2即可,解得:a<-$\frac{1}{2}$,
综上:a的范围是:$(-∞\;,\;\;-\frac{1}{2})∪\{0\}$,
故答案为:(-∞,-$\frac{1}{2}$)∪{0}.
点评 本题考查了函数的零点问题,考查二次函数的性质,是一道基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.设数列{an}中,已知a1=1,an=$\frac{1}{2{a}_{n-1}}$(n>1),则a2=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2 |
20.复数3-i在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, .
. ,
, ,
, 成等差数列时,求
成等差数列时,求 为
为 边的中点,求线段
边的中点,求线段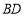 长的最小值.
长的最小值.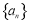 中,
中, ,
, ,则
,则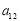 的值是( )
的值是( ) 如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.
如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.