题目内容
5. 如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.
如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.(1)证明:AE⊥BD1;
(2)求点C到平面ABD1的距离.
分析 (1)过点D1作D1O⊥AE,交AE于点O,连结BO,由已知得D1O⊥平面ABCE,AD1=$\sqrt{2}$,D1E=1,AE=BE=$\sqrt{3}$,D1O=$\frac{\sqrt{2}×1}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,AO=$\sqrt{2-\frac{2}{3}}$=$\frac{2\sqrt{3}}{3}$,EO=$\sqrt{1-\frac{2}{3}}$=$\frac{\sqrt{3}}{3}$,求出BO,从而得到AO⊥BO,进而得到AE⊥平面BOD1,由此能证明AE⊥BD1.
(2)点C到平面ABD1的距离等于点E到平面ABD1的距离,利用等体积求点C到平面ABD1的距离.
解答  (1)证明:过点D1作D1O⊥AE,交AE于点O,连结BO,
(1)证明:过点D1作D1O⊥AE,交AE于点O,连结BO,
∵点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,
将△ADE沿AE折起到△AD1E的位置,使得D1-AE-B为直二面角,
∴D1O⊥平面ABCE,AD1=$\sqrt{2}$,D1E=1,AE=BE=$\sqrt{3}$,
D1O=$\frac{\sqrt{2}×1}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,AO=$\sqrt{2-\frac{2}{3}}$=$\frac{2\sqrt{3}}{3}$,
EO=$\sqrt{1-\frac{2}{3}}$=$\frac{\sqrt{3}}{3}$,
cos∠BAO=$\frac{4+3-3}{2×2×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
BO=$\sqrt{4+\frac{4}{3}-2×2×\frac{2\sqrt{3}}{3}×\frac{\sqrt{3}}{3}}$=$\frac{2\sqrt{6}}{3}$,
∴AO2+BO2=AB2,∴AO⊥BO,
∴∠BOD1是直二面角D1-AE-B的平面角,
∴∠BOD1=90°,
∵BO⊥AE,D1O⊥AE,BO∩OD1=O,
∴AE⊥平面BOD1,∵BD1?平面BOD1,
∴AE⊥BD1.
(2)解:∵CE∥AB,
∴点C到平面ABD1的距离等于点E到平面ABD1的距离,设为h,
则由等体积可得$\frac{1}{3}×\frac{1}{2}×2×\sqrt{2}×\frac{\sqrt{6}}{3}$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×1$h,
∴h=$\frac{2\sqrt{6}}{3}$,
∴点C到平面ABD1的距离等于$\frac{2\sqrt{6}}{3}$.
点评 本题考查异面直线垂直的证明,考查点C到平面ABD1的距离的求法,解题时要认真审题,注意等体积法的合理运用.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案 “开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目,选手面对1-8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:20-30;30-40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)填写下面2×2列联表:判断是否有90%的把握认为猜对歌曲名称是否与年龄有关,说明你的理由:(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 年龄/正误 | 正确 | 错误 | 合计 |
| 20-30 | |||
| 30-40 | |||
| 合计 |
若某人在点 测得金字塔顶端仰角为
测得金字塔顶端仰角为 ,此人往金字塔方向走了80米到达点
,此人往金字塔方向走了80米到达点 ,测得金字塔顶端的仰角为
,测得金字塔顶端的仰角为 ,则金字塔的高度最接近于(忽略人的身高)(参考数据
,则金字塔的高度最接近于(忽略人的身高)(参考数据 )( )
)( )
A.110米 B.112米
C.220米 D.224米
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 ,函数
,函数 的定义域为
的定义域为 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
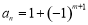 B.
B.
 D.
D.
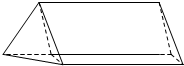 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.