题目内容
17.已知函数f(x)=$\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x-\frac{1}{2}$,x∈R.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)的单调区间.
分析 (Ⅰ)由条件利用三角恒等变换化简函数的解析式,求得函数的最小正周期.
(Ⅱ)由条件利用正弦函数的单调性,求得f(x)的单调区间.
解答 解:(Ⅰ)∵函数f(x)=$\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x-\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x=sin(2x+$\frac{π}{6}$),
故函数的最小正周期为$\frac{2π}{2}$=π.
(Ⅱ)对于函数f(x)=sin(2x+$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,可得函数的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
可得函数的增区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,属于基础题.

练习册系列答案
相关题目
8.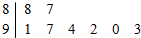 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
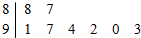 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91.5、5 | B. | 91、5 | C. | 92、5.5 | D. | 92、5 |
2.下列函数中,是偶函数且在区间(0,+∞)上是减函数的是( )
| A. | $f(x)=\frac{1}{x^2}$ | B. | f(x)=x2 | C. | $f(x)=\frac{1}{x}$ | D. | f(x)=lnx |
6.对任意$x∈({0,\frac{π}{2}})$,不等式sinx•f(x)<cosx•f′(x)恒成立,则下列不等式错误的是( )
| A. | $f({\frac{π}{3}})>\sqrt{2}f({\frac{π}{4}})$ | B. | $f({\frac{π}{3}})>2cos1•f(1)$ | C. | $f({\frac{π}{4}})<\sqrt{2}cos1•f(1)$ | D. | $f({\frac{π}{4}})<\frac{{\sqrt{6}}}{2}f({\frac{π}{6}})$ |