题目内容
【题目】已知函数
（1）若
，求函数在点
处的切线方程；
（2）求函数的单调区间；
（3）若
，任取
存在实数
使
恒成立，求的取值范围．
【答案】（1）
（2）见解析（3）
【解析】分析：第一问首先将
代入函数解析式，之后应用求导公式求得其导数，将
代入，求得其函数值和导函数值，之后应用点斜式将切线方程写出，在化为一般式即可；第二问对函数求导，对导数等于零的根的大小进行比较，分类讨论求得其单调区间；第三问从函数解析式可以发现，
为函数的两个零点，之后将问题转化为最值来处理即可求得结果.
详解：（1）
由已知
切线斜率
， 
切线方程
即 
（2）令
，
即
当
时，
在R上为增函数
当
时， 
，在
上为增函数，在
上为减函数
当
时， 
，在
上为增函数，在
上为减函数
（3） 时，
，
，
，由（2）可知在
内有最小值
，要使
恒成立，
大于等于
最大值即
的取值范围是
.
【题目】近年来，我国大力发展新能源汽车工业，新能源汽车（含电动汽车）销量已跃居全球首位.某电动汽车厂新开发了一款电动汽车，并对该电动汽车的电池使用情况进行了测试，其中剩余电量
与行驶时间
（单位：小时）的测试数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如果剩余电量不足
，则电池就需要充电.
（1）从
组数据中选出
组作回归分析，设
表示需要充电的数据组数，求的分布列及数学期望；
（2）根据电池放电的特点，剩余电量与时间工满足经验关系式：
，通过散点图可以发现与之间具有相关性.设
，利用表格中的前组数据求相关系数
的把握认为与
之间具有线性相关关系.（当相关系数满足
时，则认为的把握认为两个变量具有线性相关关系）；
（3）利用与的相关性及前组数据求出与工的回归方程.（结果保留两位小数）
附录：相关数据：
，
，
，
.
前9组数据的一些相关量：
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
|
|
|
|
相关公式：对于样本
.其回归直线
的斜率和截距的最小二乘估计公式分别为：
，
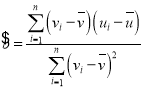，相关系数
.
【题目】一鲜花店一个月（30天）某种鲜花的日销售量与销售天数统计如下：
日销售量（枝） | 0～49 | 50～99 | 100～149 | 150～199 | 200～250 |
销售天数（天） | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率．
（1）试求这30天中日销售量低于100枝的概率；
（2）若此花店在日销售量低于100枝的6天中选择2天作促销活动，求这2天的日销售量都低于50枝的概率（不需要枚举基本事件）．
