Question

【题目】已知A(－2，0)，B(2，0)为椭圆C的左、右顶点，F为其右焦点，P是椭圆C上异于A，B的动点，且△APB面积的最大值为。

(Ⅰ)求椭圆C的方程；

(Ⅱ)直线AP与椭圆在点B处的切线交于点D，当点P在椭圆上运动时，求证：以BD为直径的圆与直线PF恒相切．

Answer 1

【答案】（Ⅰ）椭圆C的方程为（Ⅱ）见解析

【解析】

（1）根据题意得到a,b,c的方程组，解方程组即得椭圆C的方程.(2)求证圆心到直线PF的距离等于|BD|，即证以BD为直径的圆与直线PF恒相切．

（1）由题意可设椭圆C的方程为 (a>b>0)，F(c，0)．

由题意知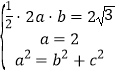，解得b=，c=1.

故椭圆C的方程为，离心率为。

（2）证明：由题意可设直线AP的方程为y=k(x+2)(k≠0)。

则点D坐标为（2,4k）,BD中点E的坐标为（2，2k）.

由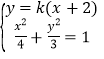得

设点P的坐标为，则

所以

因为点F坐标为(1，0)，

当k＝±时，点P的坐标为，直线PF⊥x轴，点D的坐标为(2，±2)．

此时以BD为直径的圆(与直线PF相切．

当时，则直线PF的斜率，

所以直线PF的方程为，

点E到直线PF的距离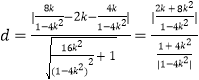

又因为|BD|＝4|k|，所以d＝|BD|.

故以BD为直径的圆与直线PF相切．

综上得，当点P在椭圆上运动时，以BD为直径的圆与直线PF恒相切．