题目内容
已知函数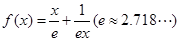 .
.
(1)若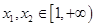 ,
,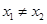 ,求证:
,求证: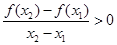 ;
;
(2)若实数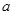 满足
满足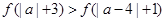 .试求
.试求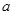 的取值范围.
的取值范围.
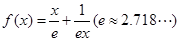 .
.(1)若
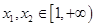 ,
,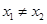 ,求证:
,求证: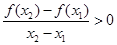 ;
;(2)若实数
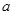 满足
满足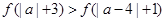 .试求
.试求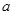 的取值范围.
的取值范围.(1)利用作差法证明,(2)
试题分析:(Ⅰ)由
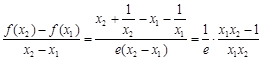 ,
,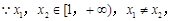
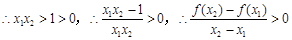 . (5分)
. (5分)(Ⅱ)由(Ⅰ)可知
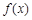 在
在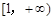 上为增函数,
上为增函数,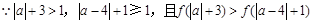 ,
,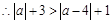 .
.当
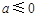 时,
时,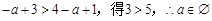 ;
;当
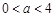 时,
时,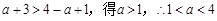 ;
;当
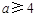 时,
时,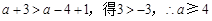 ,
,综上所述,实数
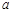 的取值范围为
的取值范围为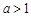 .
.点评:解含参的绝对值不等式时,常常利用分类讨论法去掉绝对值,将不等式转化为一般不等式求解

练习册系列答案
相关题目
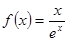 的一个单调递增区间是( )
的一个单调递增区间是( )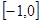

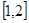
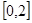
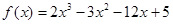 在
在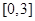 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( ) 
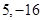
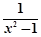 在区间(1,+∞)上的单调性,并用单调性定义证明.
在区间(1,+∞)上的单调性,并用单调性定义证明.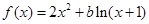 ,其中
,其中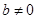 .
.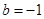 时,求在曲线
时,求在曲线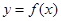 上一点
上一点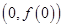 处的切线方程;
处的切线方程;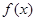 的极值点。
的极值点。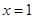 是函数
是函数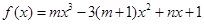 的一个极值点,其中
的一个极值点,其中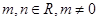
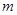 与
与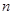 的关系式;
的关系式; 的单调区间;
的单调区间;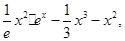
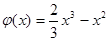 ;试比较g(x)与
;试比较g(x)与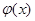 的大小。
的大小。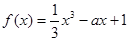 .
.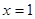 时,
时,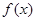 取得极值,求实数
取得极值,求实数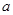 的值;
的值;
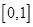 上的最小值;
上的最小值;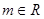 ,直线
,直线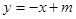 都不是曲线
都不是曲线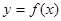 的切线,求实数
的切线,求实数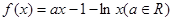
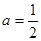 时,求函数在
时,求函数在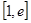 上的最大值和最小值;
上的最大值和最小值;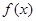 在
在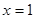 处取得极值,不等式
处取得极值,不等式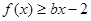 对
对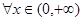 恒成立,求实数
恒成立,求实数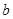 的取值范围。
的取值范围。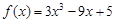 .
.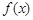 的单调递增区间;
的单调递增区间;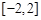 上的最大值和最小值.
上的最大值和最小值.