题目内容
判断函数f(x)=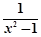 在区间(1,+∞)上的单调性,并用单调性定义证明.
在区间(1,+∞)上的单调性,并用单调性定义证明.
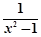 在区间(1,+∞)上的单调性,并用单调性定义证明.
在区间(1,+∞)上的单调性,并用单调性定义证明.f(x)在区间(1,+∞)上是减函数.利用定义证明
试题分析:f(x)在区间(1,+∞)上是减函数.证明如下: 2分
取任意的x1,x2∈(1,+∞),且x1<x2,则 3分
f(x1)-f(x2)=
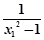 -
-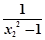 =
=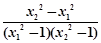 =
=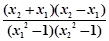 . 5分
. 5分∵x1<x2,∴x2-x1>0. 6分
又∵x1,x2∈(1,+∞),∴x2+x1>0,
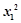 -1>0,
-1>0,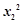 -1>0, 8分
-1>0, 8分∴(
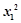 -1)(
-1)(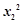 -1)>0.(x2+x1)(x2-x1)>0 10分
-1)>0.(x2+x1)(x2-x1)>0 10分∴f(x1)-f(x2)>0. 11分
根据定义知:f(x)在区间(1,+∞)上是减函数. 12分
点评:熟练掌握定义法证明函数的单调性的步骤是解决此类问题的关键,属基础题

练习册系列答案
相关题目
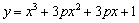 .
. 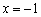 处取到极值?若有可能,求实数
处取到极值?若有可能,求实数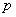 的值;否则说明理由;
的值;否则说明理由;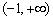 上为增函数,求实数
上为增函数,求实数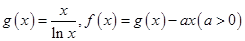 .
.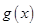 的单调区间;
的单调区间;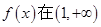 上是减函数,求实数
上是减函数,求实数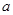 的最小值;
的最小值;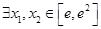 ,使
,使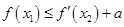 成立,求实数
成立,求实数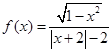 (2)
(2)


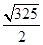
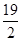
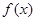 的定义域为
的定义域为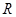 ,若存在常数
,若存在常数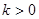 ,使
,使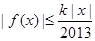 对一切实数
对一切实数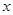 均成立
均成立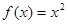 ;②
;②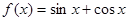 ;③
;③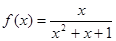 ;④
;④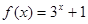 .
.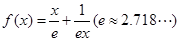 .
.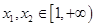 ,
,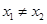 ,求证:
,求证: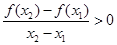 ;
;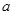 满足
满足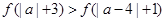 .试求
.试求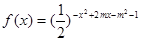 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数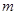 的取
的取
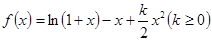
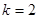 时,求曲线
时,求曲线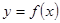 在点
在点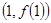 处的切线方程。
处的切线方程。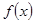 的单调区间
的单调区间