题目内容
已知函数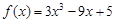 .
.
(Ⅰ)求函数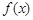 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数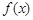 在
在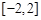 上的最大值和最小值.
上的最大值和最小值.
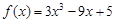 .
.(Ⅰ)求函数
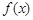 的单调递增区间;
的单调递增区间;(Ⅱ)求函数
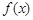 在
在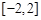 上的最大值和最小值.
上的最大值和最小值.(1)函数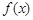 的单调增区间为
的单调增区间为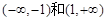
(2)当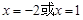 时,函数
时,函数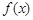 取得最小值
取得最小值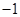 .
.
当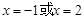 时,函数
时,函数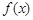 取得最大值11
取得最大值11
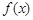 的单调增区间为
的单调增区间为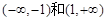
(2)当
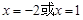 时,函数
时,函数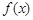 取得最小值
取得最小值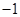 .
.当
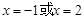 时,函数
时,函数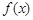 取得最大值11
取得最大值11试题分析:解:(1)
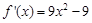 . 2分
. 2分令
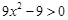 , 4分
, 4分解此不等式,得
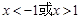 .
. 因此,函数
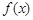 的单调增区间为
的单调增区间为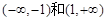 . 6分
. 6分(2) 令
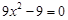 ,得
,得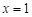 或
或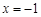 . 8分
. 8分当
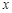 变化时,
变化时,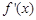 ,
,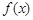 变化状态如下表:
变化状态如下表: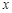 | -2 | 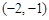 | -1 | 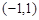 | 1 | 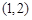 | 2 |
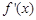 | 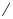 | + | 0 | - | 0 | + | 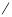 |
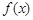 | -1 |  | 11 | 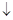 | -1 |  | 11 |
从表中可以看出,当
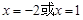 时,函数
时,函数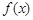 取得最小值
取得最小值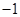 .
.当
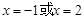 时,函数
时,函数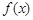 取得最大值11. 14分
取得最大值11. 14分点评:结合导数的符合判定函数单调性,进而求解最值,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.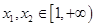 ,
,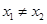 ,求证:
,求证: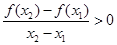 ;
;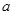 满足
满足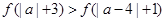 .试求
.试求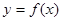 在R上是增函数,且
在R上是增函数,且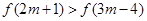 ,则
,则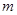 的取值范围是( )
的取值范围是( ) 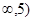
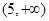
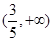
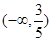
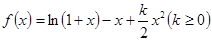
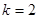 时,求曲线
时,求曲线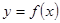 在点
在点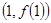 处的切线方程。
处的切线方程。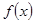 的单调区间
的单调区间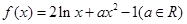
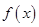 的单调区间;
的单调区间;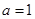 ,试分别解答以下两小题.
,试分别解答以下两小题.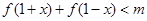 对任意的
对任意的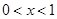 恒成立,求实数
恒成立,求实数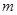 的取值范围;
的取值范围;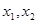 是两个不相等的正数,且
是两个不相等的正数,且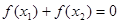 ,求证:
,求证: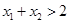 .
.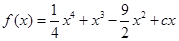 有三个极值点。
有三个极值点。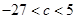 ;
;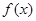 在区间
在区间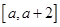 上单调递减,求
上单调递减,求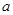 的取值范围。
的取值范围。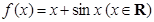 ( )
( )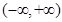 上是减函数
上是减函数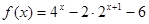 ,其中
,其中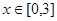 。
。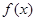 的最大值和最小值;
的最大值和最小值;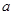 满足:
满足: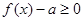 恒成立,求
恒成立,求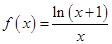 。
。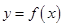 在
在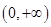 上的单调性;
上的单调性;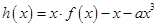 在
在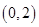 上有极值,求
上有极值,求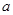 的取值范围。
的取值范围。