题目内容
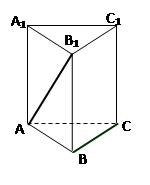
、正方体ABCD，A1B1C1D1中，E、F分别是BB1、CC1的中点，则AE、BF所成的角的余弦值是（）
A． | B． | C． | D． |
C
分析：取DD1的中点G，∠GAD为AE、BF所成的角，在△GAD中，用勾股定理求得三边长，余弦定理求得cos∠EAG 的值．
解答：解：取DD1的中点G，由GA∥BF 且GA="BF" 可得∠GAD为AE、BF所成的角，设正方体棱长为1，△GAD中，利用勾股定理可得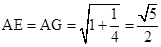
． 又EG=
，
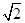由余弦定理可得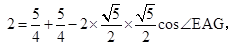
，
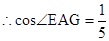故选 C．
解答：解：取DD1的中点G，由GA∥BF 且GA="BF" 可得∠GAD为AE、BF所成的角，设正方体棱长为1，△GAD中，利用勾股定理可得
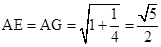． 又EG=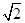，由余弦定理可得
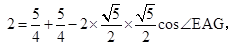
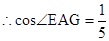，故选 C．
练习册系列答案
相关题目
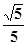
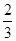
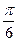.∠AOQ＝α，α∈[0，π）.（Ⅰ）若Q（
，
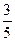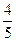），求cos（α－
·
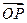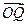，求f（α）的值域．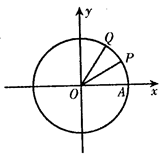
的底面边长为2，高 
与AD所成角的大小是______________
所成的角是 、直线
和平面
所成的角为 .