题目内容
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
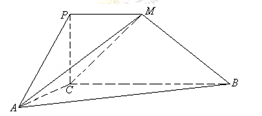
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.

(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
(1)详见解析;(2)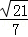 ;(3)
;(3)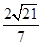
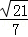 ;(3)
;(3)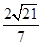
试题分析:(1)先根据线面垂直的判定定理证PC⊥平面ABC,即可证得PC⊥AC。(2)用空间向量法求二面角。先过C作BC的垂线,建立空间直角坐标系,再求各点的坐标,和各向量的坐标,再根据向量垂直的数量积公式求面的法向量,但需注意两法向量所成的角和二面角相等或互补。(3)在(2)中已求出面
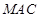 的一个法向量
的一个法向量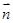 ,根据
,根据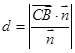 可求其距离。
可求其距离。试题解析:解:(1)证明:∵PC⊥BC,PC⊥AB,
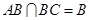 ∴PC⊥平面ABC,∵
∴PC⊥平面ABC,∵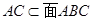 ∴PC⊥AC. 2分
∴PC⊥AC. 2分(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.
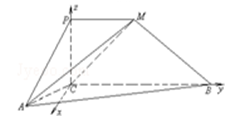
设P(0,0,z),则
 .
.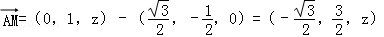 .
.∵
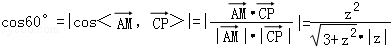 ,
,且z>0,∴
 ,得z=1,∴
,得z=1,∴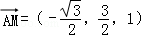 .
.设平面MAC的一个法向量为
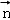 =(x,y,1),则由
=(x,y,1),则由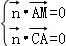
得
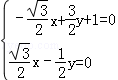 得
得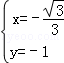 ∴
∴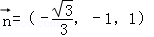 .
.平面ABC的一个法向量为
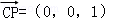 .
.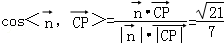 .
.显然,二面角M﹣AC﹣B为锐二面角,∴二面角M﹣AC﹣B的余弦值为
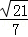 . 8分
. 8分(3)点B到平面MAC的距离
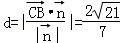 . 12分
. 12分
练习册系列答案
相关题目


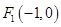 、
、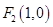 ,动点
,动点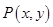 ,且满足
,且满足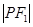 、
、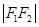 、
、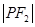
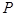 的轨迹
的轨迹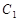 的方程;
的方程;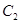 的方程为
的方程为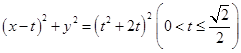 ,过点
,过点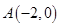 的直线
的直线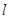 与曲线
与曲线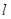 被曲线
被曲线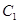 截得的线段长的最小值.
截得的线段长的最小值.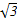
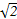
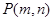 是直线
是直线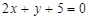 上的任意一点,则
上的任意一点,则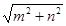 的最小值为
的最小值为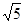
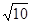
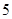
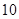
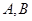 分别是
分别是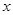 轴、
轴、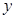 轴上两个动点,又有一定点
轴上两个动点,又有一定点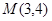 ,则
,则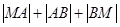 的最小值是( )
的最小值是( )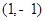 到直线
到直线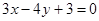 的距离为( )
的距离为( )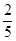
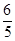
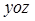 内的射影,则OB等于( )
内的射影,则OB等于( )