题目内容
【题目】已知抛物线![]() 的焦点在抛物线
的焦点在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)过点![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线,![]() 、
、![]() 分别为两个切点,求
分别为两个切点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() 的方程为
的方程为![]() 其准线方程为
其准线方程为![]() ;(2)2
;(2)2
【解析】试题分析:(1)求得抛物线C1的焦点,由题意可得p=2,即可得到所求抛物线的方程和准线方程;(2)设P(2t,t2),A(x1,y1),B(x2,y2),求出y=x2+1的导数,可得切线PA,PB的斜率和方程,又PA和PB都过P点,可得直线AB的方程,代入抛物线y=x2+1,运用韦达定理和弦长公式,由点到直线的距离公式,可得P到直线AB的距离,再由三角形的面积公式,化简整理计算可得所求面积的最小值.
试题解析:
(1)![]() 的方程为
的方程为![]() 其准线方程为
其准线方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,
,
则切线![]() 的方程:
的方程:![]() ,即
,即![]() ,又
,又![]() ,
,
所以![]() ,同理切线
,同理切线![]() 的方程为
的方程为![]() ,
,
又![]() 和
和![]() 都过
都过![]() 点,所以
点,所以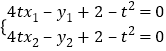 ,
,
所以直线![]() 的方程为
的方程为![]() .
.
联立![]() 得
得![]() ,所以
,所以![]() 。
。
所以![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
所以![]() 的面积
的面积![]()
所以当![]() 时,
时, ![]() 取最小值为
取最小值为![]() 。即
。即![]() 面积的最小值为2.
面积的最小值为2.

【题目】【2018四川南充高三第二次(3月)高考适应性考试】某校开展“翻转合作学习法”教学试验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的![]() 列联表:
列联表:
成绩优秀 | 成绩一般 | 合计 | |
对照班 | 20 | 90 | 110 |
翻转班 | 40 | 70 | 110 |
合计 | 60 | 160 | 220 |
(I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(II)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到1名“对照班”学生交流的概率.
附表:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中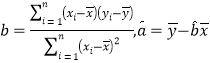 .
.