题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)易知△![]() 与△
与△![]() 均为等边三角形,点
均为等边三角形,点![]() 为
为![]() 的中点,可得
的中点,可得![]() ,
,![]() ,进而得
,进而得![]() 平面
平面![]() ,从而得证;
,从而得证;
(2)由勾股定理可得![]() ,从而以点
,从而以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,分别求平面
轴建立空间直角坐标系,分别求平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量,利用法向量求解二面角即可..
的一个法向量,利用法向量求解二面角即可..
试题解析:
(1)证明:设点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,由
,由![]() ,
,![]() ,知△
,知△![]() 与△
与△![]() 均为等边三角形,点
均为等边三角形,点![]() 为
为![]() 的中点,可得
的中点,可得![]() ,
,![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
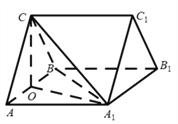
(2)由(1)知△![]() 与△
与△![]() 均是边长为
均是边长为![]() 是等边三角形,
是等边三角形,![]() ,又在△
,又在△![]() 中
中![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,所以
,所以![]() ,故
,故![]()
![]() ,
,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
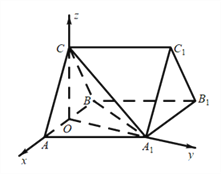
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
![]() ,得
,得![]() ,同理可得平面
,同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由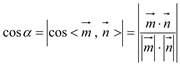
![]()
![]() ,
,
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某地一商场记录了![]() 月份某
月份某![]() 天当中某商品的销售量
天当中某商品的销售量![]() (单位:
(单位:![]() )与该地当日最高气温
)与该地当日最高气温![]() (单位:
(单位:![]() )的相关数据,如下表:
)的相关数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)试求![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月某日的最高气温是
月某日的最高气温是![]() ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;
(3)假定该地![]() 月份的日最高气温
月份的日最高气温![]() ,其中
,其中![]() 近似取样本平均数
近似取样本平均数![]() ,
,![]() 近似取样本方差
近似取样本方差![]() ,试求
,试求![]() .
.
附:参考公式和有关数据 ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() .
.
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计数据表明,样本中所有人每天用于阅读的时间(简称阅读用时)都不超过3小时,其频数分布表如下:(用时单位:小时)
用时分组 |
|
|
|
|
|
|
频数 | 10 | 20 | 50 | 60 | 40 | 20 |
(1)用样本估计总体,求该市市民每天阅读用时的平均值;
(2)为引导市民积极参与阅读,有关部门牵头举办市读书经验交流会,从这200人中筛选出男女代表各3名,其中有2名男代表和1名女代表喜欢古典文学.现从这6名代表中任选2名男代表和2名女代表参加交流会,求参加交流会的4名代表中,喜欢古典文学的男代表多于喜欢古典文学的女代表的概率.



