题目内容
(本小题满分12分)
已知f (x)=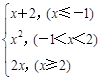 .
.
(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
已知f (x)=
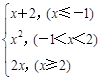 .
.(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
(1)(-∞,+∞);(2)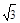 ;(3)见解析。
;(3)见解析。
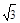 ;(3)见解析。
;(3)见解析。试题分析:(1)注意分段函数定义域和值域的求法和要求,第一段值域为(-∞,1],第二段值域为(0,4),
第三段值域为[4,+∞),综上,函数的值域为(-∞,+∞). ……4分
(2)g (t)=3,即t+2=3,t≤-1,不存在;
x2=3,-1<x<2,解得:x=
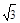 ,即t=
,即t=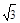 ;
;2x=3,x≥2,x不存在.
综上,t的值为
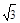 . ……8分
. ……8分(3)因为函数在[2,+∞)上的解析式为f (x)=2x,任取x1,x2∈[2,+∞),且x1<x2,则
f (x1)-f (x2)=2x1-2x2=2(x1-x2)<0,所以函数在[2,+∞)上单调递增. ……12分
点评:分段函数的值域是各段表达式的y值的并集。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是定义域R上的奇函数,且当
是定义域R上的奇函数,且当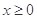 时,
时,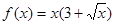 则当
则当 时,
时,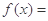 ____________________
____________________ 满足:
满足: ,则
,则 .
. ,正实数
,正实数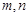 满足
满足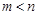 ,且
,且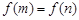 ,若
,若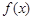 在区间
在区间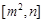 上的最大值为2,则
上的最大值为2,则 的值为( )
的值为( )
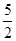
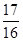

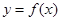 的图像向左平移2个单位得到函数
的图像向左平移2个单位得到函数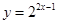 的图像,则函数的解析表达式为
的图像,则函数的解析表达式为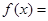 .
.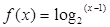 。
。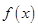 的零点;
的零点;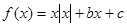 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有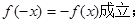 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数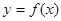 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞), 且
且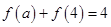 ,那么
,那么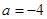 ;
;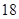 ,
,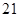 ,
,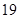 ,
,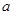 ,
,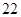 的平均数是
的平均数是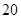 ,那么这组数据的方差是
,那么这组数据的方差是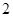 ;
; 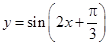 的图象,只要将
的图象,只要将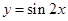 的图象向左平移
的图象向左平移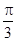 单位;
单位;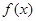 在
在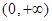 为增函数,且
为增函数,且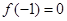 ,则不等式
,则不等式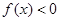 的解集为
的解集为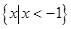 .
.