题目内容
(本题满分12分)已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0,②f(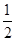 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),
都有f(xy)= f(x)+ f(y),求不等式f(x)+ f(5-x)≥-2的解集。
①x>1时,f(x)<0,②f(
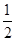 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),都有f(xy)= f(x)+ f(y),求不等式f(x)+ f(5-x)≥-2的解集。
 。
。试题分析:(1)构造函数中两个任意变量的函数值差,结合函数表达式得到函数单调性的证明。
(2)结合特殊值的函数值,得到f(4)=-2,进而得到函数的不等式的求解。
解:设0<x1<x2,则
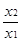 >1,∵f(xy)= f(x)+ f(y)
>1,∵f(xy)= f(x)+ f(y)∴f(x2)= f(
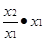 )= f(
)= f(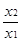 )+ f(x1)
)+ f(x1)又∵x>1时,f(x)<0,∴f(
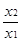 )<0
)<0∴f(x2)<f(x1),∴f(x)是( 0,+∞)上的减函数。又∵f(1)= f(1)+ f(1)
∴f(1)=0,而f(
 )=1,∴f(2?
)=1,∴f(2? )= f(2)+ f(
)= f(2)+ f( )=0
)=0∴f(2)=-1,∴f(x)+ f(5-x)≥-2="2" f(2)= f(4)
∴
 ,∴0<x≤1,或4≤x<5
,∴0<x≤1,或4≤x<5∴原不等式的解集是
 。
。点评:解决该试题的关键是能利用已知条件分析得到函数的单调性的证明,结合已知的关系式将所求的表示为一个整体函数式,同时能结合单调性得到求解。

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
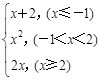 .
. ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( ) 的方程
的方程 ,给出下列四个题:
,给出下列四个题: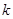 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根; ,则
,则 的解集
的解集 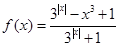
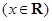 的最大值为
的最大值为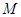 ,最小值为
,最小值为 ,
, 的值为 .
的值为 .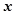 的函数
的函数 ,有下列结论:
,有下列结论: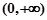 ;②该函数是奇函数;
;②该函数是奇函数;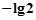 ; ④当
; ④当 时
时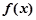 为增函数,当
为增函数,当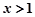 时
时 ,
,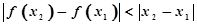 恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )
恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )