题目内容
设函数 是定义域R上的奇函数,且当
是定义域R上的奇函数,且当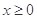 时,
时,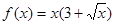 则当
则当 时,
时,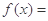 ____________________
____________________
 是定义域R上的奇函数,且当
是定义域R上的奇函数,且当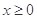 时,
时,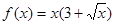 则当
则当 时,
时,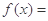 ____________________
____________________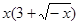
试题分析:当
 时,
时,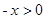 ,所以
,所以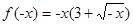 ,又因为
,又因为 是定义域R上的奇函数,所以
是定义域R上的奇函数,所以
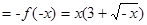 。
。点评:此类问题的一般做法是:? ①“求谁设谁”?即在哪个区间求解析式,x就设在哪个区间内; ②要利用已知区间的解析式进行代入; ③利用f(x)的奇偶性写出-f(x)或f(-x)?从而解出f(x)。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
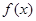 满足
满足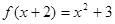 , 则
, 则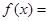 .
. 米.
米.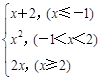 .
. .
.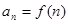 ,写出数列
,写出数列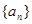 的前5项;
的前5项;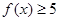 .
.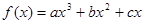 在点
在点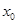 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数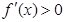 的
的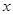 的取值范围为(1,3)
的取值范围为(1,3)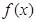 的解析式及
的解析式及 时,求
时,求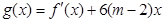 的最大值。
的最大值。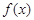 ,
,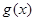 满足
满足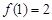 ,
,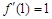 ,
,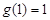 ,
,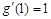 ,则函数
,则函数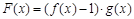 的图象在
的图象在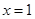 处的切线方程为 .
处的切线方程为 . 内修建一个矩形
内修建一个矩形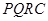 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且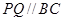 ,
,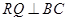 ,另外
,另外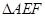 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量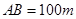 ,
,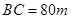 ,
, 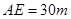 ,
,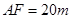 .
.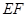 的方程;
的方程;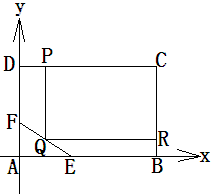
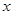 的方程
的方程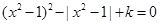 ,给出下列四个题:
,给出下列四个题: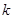 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;