题目内容
13.下列函数中,表示相等函数的一组是( )| A. | y=$\sqrt{x^2}$,y=|x| | B. | y=$\frac{x^2}{x}$,y=x | ||
| C. | y=$\sqrt{x^2}$,$y={(\sqrt{x})^2}$ | D. | y=$\sqrt{x+1}•\sqrt{x-1}$,y=$\sqrt{{x^2}-1}$ |
分析 判断函数的定义域与对应法则是否相同,推出结果即可.
解答 解:y=$\sqrt{x^2}$=|x|,y=|x|函数的定义域相同,对应法则相同,是相同函数.
y=$\frac{x^2}{x}$,y=x的定义域不相同,不是相同函数;
y=$\sqrt{x^2}$,$y={(\sqrt{x})}^{2}$的定义域不相同,不是相同函数;
y=$\sqrt{x+1}•\sqrt{x-1}$,y=$\sqrt{{x^2}-1}$,的定义域不相同,不是相同函数;
故选:A.
点评 本题是基础题,函数的定义的应用,考查分析问题解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.函数f(x)=$\frac{1}{{\sqrt{2-{{log}_2}(1-x)}}}$的定义域为( )
| A. | (-3,+∞) | B. | $(-∞,\frac{1}{2})$ | C. | (-3,1) | D. | (0,1) |
2.下列各式中正确的是( )
| A. | 0=∅ | B. | ∅={0} | C. | 0∈∅ | D. | ∅⊆{0} |
3.设a=30.2,b=0.23,c=log0.23,则a,b,c的大小关系是( )
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | a>b>c |
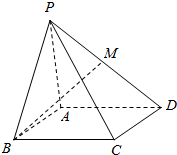 如图.在四棱锥P-ABCD中,∠PAD=90°,PA⊥CD.点M是棱PD的中点.
如图.在四棱锥P-ABCD中,∠PAD=90°,PA⊥CD.点M是棱PD的中点.