题目内容
【题目】已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1﹣bn)an}的前n项和为2n2+n.
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(1)运用等差数列的中项性质和等比数列的通项公式,解方程可得首项和公比,进而得到所求通项公式;
(2)设cn=(bn+1﹣bn)an,数列{cn}前n项和为Sn.由数列的递推式求得cn,再由数列的恒等式可得bn,再由数列的错位相减法求和,结合等比数列的求和公式,计算可得所求通项公式.
(1)由题知a3+a4+a5=28,a4+2是a3,a5的等差中项,
所以a3+a5=2a4+4,解得a4=8,a3+a5=20,
即a1q3=8,a1q2+a1q4=20,
解得a1=1,q=2,
所以![]() ;
;
(2)设cn=(bn+1﹣bn)an,数列{cn}前n项和为Sn.
由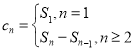 ,Sn=2n2+n,Sn﹣1=2(n﹣1)2+n﹣1.
,Sn=2n2+n,Sn﹣1=2(n﹣1)2+n﹣1.
解得cn=4n﹣1.
由(1)可知![]() ,
,
所以![]() ,
,
故![]() ,
,
bn﹣b1=(bn﹣bn﹣1)+(bn﹣1﹣bn﹣2)+…+(b3﹣b2)+(b2﹣b1)![]() ,
,
设![]() ,
,
所以![]() ,
,
相减可得![]()
![]() 3+4
3+4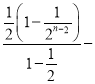 (4n﹣5)(
(4n﹣5)(![]() )n﹣1,
)n﹣1,
化简可得![]() ,
,
又b1=1,所以![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目