题目内容
【题目】已知函数![]() ,其中
,其中![]() ;
;
(l)判断函数![]() 是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
(2)讨论在![]() 上函数
上函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析;(2)见解析
【解析】
(1) ![]() ,设
,设![]() ,
,![]() ,因此
,因此![]() 单调递减,
单调递减,![]() ,讨论
,讨论![]() 正负即可判断出极值情况;
正负即可判断出极值情况;
(2)由(1)可知若![]() 时,
时,![]() 恒为增函数,计算可知
恒为增函数,计算可知![]() ,此时无零点, 若
,此时无零点, 若![]() 时,
时, ![]() ,可求得
,可求得![]() ,讨论
,讨论![]() 与
与![]() 的关系,及若
的关系,及若![]() ,
,![]() ,函数在区间
,函数在区间![]() 的单调性及函数值在区间端点的符号,即可得出结论.
的单调性及函数值在区间端点的符号,即可得出结论.
(1)![]() ,设
,设![]() ,
,
![]() ,因此
,因此![]() 单调递减,
单调递减,
![]() ,
,
又![]() 时,
时,![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() ,使
,使![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 在
在![]() 处取极大值,不存在极小值.
处取极大值,不存在极小值.
若![]() ,即
,即![]() ,
,![]() ,
,
![]() 在
在![]() 单调递增,此时
单调递增,此时![]() 无极值.
无极值.
(2)由第一问结论可知:
(i)若![]() 时,由上问可知:
时,由上问可知:
![]() ,
,
即![]() 时函数没有零点.
时函数没有零点.
(ii)若![]() 时,
时,![]() 时
时![]() 单调递增;
单调递增;
![]() 时,
时,![]() 单调递减.
单调递减.
由![]() ,得
,得![]() ,
,
从而![]() ,再设
,再设![]() ,
,
则![]() ,从而a关于
,从而a关于![]() 单调递增.
单调递增.
①若![]() ,此时
,此时![]() ,
,
若![]() 得
得![]() 或
或![]() ,
,
所以![]() 时无零点;
时无零点;
若![]() 得
得![]() ,
,
所以![]() 时有一个零点;
时有一个零点;
当![]() ,
,![]() ,有一个零点.
,有一个零点.
因此![]() 时无零点;
时无零点;
![]() 时有一个零点;
时有一个零点;
②![]() 此时
此时![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() ,
,
若![]() 即
即![]() ,即
,即![]() 时无零点;
时无零点;
若![]() 即
即![]() ,即
,即![]() 时有一个零点.
时有一个零点.
综上所述:![]() 时无零点;
时无零点;
![]() 时有一个零点.
时有一个零点.

【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
薪资
岗位 |
|
|
|
|
数据开发 |
|
|
|
|
数据分析 |
|
|
|
|
数据挖掘 |
|
|
|
|
数据产品 |
|
|
|
|
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
【题目】桥牌是一种高雅、文明、竞技性很强的智力性游戏.近年来,在中国桥牌协会“桥牌进校园”活动的号召下,全国各地中小学纷纷积极加入到青少年桥牌推广的大营中.为了了解学生对桥牌这项运动的兴趣,某校从高一学生中随机抽取了200名学生进行调查,经统计男生与女生的人数之比为2:3,男生中有50人对桥牌有兴趣,女生中有20人对桥牌不感兴趣.
(1)完成2×2列联表,并回答能否有![]() 的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
感兴趣 | 不感兴趣 | 合计 | |
男 | 50 | —— | —— |
女 | —— | 20 | —— |
合计 | —— | —— | 200 |
(2)从被调查的对桥牌有兴趣的学生中利用分层抽样抽取6名学生,再从6名学生中抽取2名学生作为桥牌搭档参加双人赛.求抽到一名男生与一名女生的概率.
附:参考公式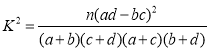 ,其中
,其中![]() .
.
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |