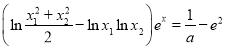题目内容
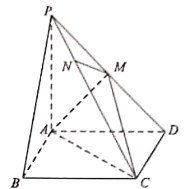
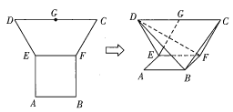
【题目】如图,在平面多边形![]() 中,
中,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析
(2)60°
【解析】
(1)先证明![]() 、
、![]() ,然后证明
,然后证明![]() 平面
平面![]() 即可;
即可;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,过点
,过点![]() 在平面
在平面![]() 内作
内作![]() 的垂线
的垂线![]() ,以
,以![]() 所在直线分别为
所在直线分别为![]() 轴建立如图所示的空间直角坐标系,然后再利用空间向量的运算求解即可.
轴建立如图所示的空间直角坐标系,然后再利用空间向量的运算求解即可.
解:(1)连接![]() ,
,
由已知,得![]() ,
,![]() ,
,
则四边形![]() 为菱形,
为菱形,
故![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]()
又![]() ,
,
所以![]() 平面
平面![]() .
.
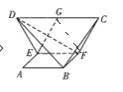
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
则易知![]() 平面
平面![]() ,
,
过点![]() 在平面
在平面![]() 内作
内作![]() 的垂线
的垂线![]() ,以
,以![]() 所在直线分别为
所在直线分别为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则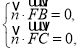 即
即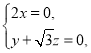 则
则![]() ,
,
取![]() ,则
,则![]() ,
,
故![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则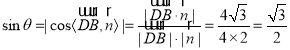 ,
,
从而直线![]() 与平面
与平面![]() 所成的角为60°.
所成的角为60°.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() ,
,![]() .
.

(1)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【题目】桥牌是一种高雅、文明、竞技性很强的智力性游戏.近年来,在中国桥牌协会“桥牌进校园”活动的号召下,全国各地中小学纷纷积极加入到青少年桥牌推广的大营中.为了了解学生对桥牌这项运动的兴趣,某校从高一学生中随机抽取了200名学生进行调查,经统计男生与女生的人数之比为2:3,男生中有50人对桥牌有兴趣,女生中有20人对桥牌不感兴趣.
(1)完成2×2列联表,并回答能否有![]() 的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
感兴趣 | 不感兴趣 | 合计 | |
男 | 50 | —— | —— |
女 | —— | 20 | —— |
合计 | —— | —— | 200 |
(2)从被调查的对桥牌有兴趣的学生中利用分层抽样抽取6名学生,再从6名学生中抽取2名学生作为桥牌搭档参加双人赛.求抽到一名男生与一名女生的概率.
附:参考公式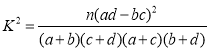 ,其中
,其中![]() .
.
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |