题目内容
【题目】如图,四棱柱![]() 中,
中,![]() 平面ABCD,四边形ABCD为平行四边形,
平面ABCD,四边形ABCD为平行四边形,![]() ,
,![]() .
.
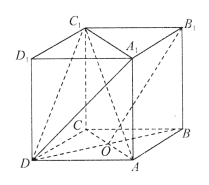
(1)若![]() ,求证:
,求证:![]() //平面
//平面![]() ;
;
(2)若![]() ,且三棱锥
,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() .
.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,根据四边形ABCD为平行四边形,可得
,根据四边形ABCD为平行四边形,可得![]() //
//![]() ,然后根据线面平行的判定定理,可得结果.
,然后根据线面平行的判定定理,可得结果.
(2)利用正弦定理,可得![]() ,进一步可得
,进一步可得![]() ,然后根据
,然后根据![]() ,可得
,可得![]() ,最后利用勾股定理,可得结果.
,最后利用勾股定理,可得结果.
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
如图
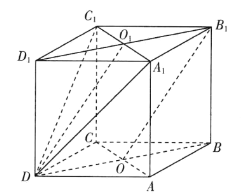
由四棱柱的性质可知![]() //
//![]() ,
,
且![]() ,则
,则![]() //
//![]() .
.
∵四边形ABCD为平行四边形,∴![]() .
.
同理![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() //
//![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]() .
.
(2)∵![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() .
.
由正弦定理可得![]() ,
,
解得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() .
.
又![]() 平面ABCD,即
平面ABCD,即![]() 平面ABCD,
平面ABCD,
∴![]() ,CD,CA两两垂直.
,CD,CA两两垂直.
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间( | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数( | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
(1)若选取的是后面4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过35人,试用(1)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: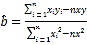
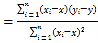 ,
,![]() .
.
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
【题目】淘汰落后产能,对生产设备进行升级改造是企业生存发展的重要前提.某企业今年对旧生产设备的一半进行了升级,剩下的一半在今后的两年内完成升级.为了分析新旧设备的生产质量,从新旧设备生产的产品中各抽取了![]() 件作为样本,对最重要的一项质量指标进行检测,该项质量指标值落在
件作为样本,对最重要的一项质量指标进行检测,该项质量指标值落在![]() 内的产品为合格品,否则为不合格品.检测数据如下:
内的产品为合格品,否则为不合格品.检测数据如下:
表1:日设备生产的产品样本频数分布表
质量指标 |
|
|
|
|
|
|
频数 | 3 | 16 | 44 | 12 | 22 | 3 |
表2:新设备生产的产品样本频数分布表
质量指标 |
|
|
|
|
|
|
频数 | 1 | 20 | 52 | 16 | 10 | 1 |
(1)根据表1和表2提供的数据,试从产品合格率的角度对新旧设备的优劣进行比较;
(2)面向市场销售时,只有合格品才能销售,这时需要对合格品的品质进行等级细分,质量指标落在![]() 内的定为优质品,质量指标落在
内的定为优质品,质量指标落在![]() 或
或![]() 内的定为一等品,其它的合格品定为二等品.完成下面的
内的定为一等品,其它的合格品定为二等品.完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与新旧设备有关;
的把握认为该企业生产的这种产品的质量指标值与新旧设备有关;
旧设备 | 新设备 | 合计 | |
优质品及一等品 | |||
二等品及不合格品 | |||
合计 | /span> |
(3)优质品每件售价![]() 元,一等品每件售价
元,一等品每件售价![]() 元,二等品每件售价
元,二等品每件售价![]() 元根据表1和表2中的数据,用该组样本中优质品、一等品、二等品各自在合格品中的频率代替从合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
元根据表1和表2中的数据,用该组样本中优质品、一等品、二等品各自在合格品中的频率代替从合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望(结果保留整数).
的分布列和数学期望(结果保留整数).
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
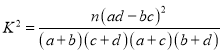 ,
,![]() .
.