题目内容
9.已知函数f(x)=lnx+$\frac{a}{x}$(a>0)(1)当a=1时,求f(x)的单调区间;
(2)如果P(x0,y0)是曲线y=f(x)上的任意一点,若以P(x0,y0)为切点的切线的斜率k≤$\frac{1}{2}$恒成立,求实数a的最小值;
(3)讨论关于x的方程f(x)=$\frac{{{x^3}+2(bx+a)}}{2x}-\frac{1}{2}$的实根的个数情况.
分析 (1)将a=1代入,求出函数的导数,从而求出函数的单调区间;
(2)先求出函数的导数,问题转化为a≥-$\frac{1}{2}$${{x}_{0}}^{2}$+x0对x0>0恒成立,从而求出a的最小值;
(3)问题转化为b=lnx-$\frac{1}{2}$x2+$\frac{1}{2}$,x>0,构造函数h(x)=lnx-$\frac{1}{2}$x2-b+$\frac{1}{2}$,通过讨论h(x)的单调性,从而判断出方程f(x)=0的根的情况.
解答 解:(1)当a=1时,$f(x)=lnx+\frac{1}{x}$,定义域为(0,+∞),…(1分)
则$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$…(2分)
令f′(x)>0,得x>1,由f′(x)<0,得0<x<1,
所以f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).…(4分)
(2)由题意,f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
以P(x0,y0)为切点的切线的斜率k满足k=f′(x0)=$\frac{{x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$(x0>0),
所以a≥-$\frac{1}{2}$${{x}_{0}}^{2}$+x0对x0>0恒成立.…(6分)
又当x0>0时,-$\frac{1}{2}$${{x}_{0}}^{2}$+x0≤$\frac{1}{2}$,所以a的最小值为$\frac{1}{2}$…(8分)
(3)由题意,方程$f(x)=\frac{{{x^3}+2(bx+a)}}{2x}-\frac{1}{2}$化简得
b=lnx-$\frac{1}{2}$x2+$\frac{1}{2}$,x>0,
令h(x)=lnx-$\frac{1}{2}$x2-b+$\frac{1}{2}$,则h′(x)=$\frac{1}{x}$-x=$\frac{(1+x)(1-x)}{x}$.
当0<x<1时,h′(x)>0,当x>1时,h′(x)<0,
所以h(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.…(10分)
所以h(x)在x=1处取得极大值,即最大值,最大值为
h(1)=ln1-$\frac{1}{2}$×12-b+$\frac{1}{2}$=-b…(11分)
所以当-b>0时,即b<0时,y=h(x)的图象与x轴恰有两个交点,
方程$f(x)=\frac{{{x^3}+2(bx+a)}}{2x}-\frac{1}{2}$有两个实根;…(12分)
当b=0时,y=h(x)的图象与x轴恰有一个交点,
方程$f(x)=\frac{{{x^3}+2(bx+a)}}{2x}-\frac{1}{2}$有一个实根;…(13分)
当b>0时,y=h(x)的图象与x轴无交点,
方程$f(x)=\frac{{{x^3}+2(bx+a)}}{2x}-\frac{1}{2}$无实根.…(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用,曲线的切线方程问题,是一道综合题.

| A. | (-3,-1) | B. | (-3,1) | C. | (-1,0) | D. | (-1,2) |
| A. | 命题“若x<1,则-≤x≤1”的逆否命题是“若x≥1,则x<-1或x≥1” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 已知命题p:?x∈R,lnx<lgx;命题q:?x0∈R,x03=1-x02,则“(¬p)∨(¬q)为真命题”. |
| A. | {x|-4<x<1} | B. | {x|-4<x<-3} | C. | {x|-3<x<1} | D. | {x|-3<x<2} |
| A. | 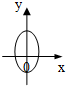 | B. | 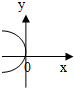 | C. | 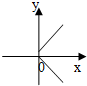 | D. | 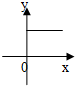 |
 在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )
在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AE}$等于( )| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{3}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |