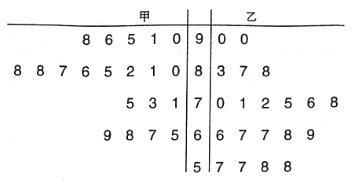
题目内容
【题目】已知数列{an}满足an+1+an=4n﹣3,n∈N*
(1)若数列{an}是等差数列,求a1的值;
(2)当a1=﹣3时,求数列{an}的前n项和Sn;
(3)若对任意的n∈N* , 都有 ![]() ≥5成立,求a1的取值范围.
≥5成立,求a1的取值范围.
【答案】
(1)解:∵an+1+an=4n﹣3,n∈N*,∴a2+a1=1,a3+a2=5,
∴a3﹣a1=5﹣1=4,设等差数列{an}的公差为d,则2d=4,解得d=2.
∴2a1+2=1,解得a1=﹣ ![]()
(2)解:∵an+1+an=4n﹣3,an+2+an+1=4n+1,∴an+2﹣an=4,a2=4.
∴数列{an}的奇数项与偶数项分别成等差数列,公差都为4.
∴a2k﹣1=﹣3+4(k﹣1)=4k﹣7;a2k=4+4(k﹣1)=4k.
∴an= ![]() ,
,
∴当n为偶数时,Sn=(a1+a2)+…+(an﹣1+an)=﹣3+9+…+(4n﹣3)= ![]() =
= ![]() .
.
当n为奇数时,Sn=Sn+1﹣an+1= ![]() ﹣2(n+1)=
﹣2(n+1)= ![]() .
.
∴Sn= 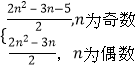
(3)解:由(2)可知:an= ![]() .
.
当n为奇数时,an=2n﹣2+a1,an+1=2n﹣1﹣a1,
由 ![]() ≥5成立,an+1+an=4n﹣3,可得:
≥5成立,an+1+an=4n﹣3,可得: ![]() ﹣a1≥﹣4n2+16n﹣10,
﹣a1≥﹣4n2+16n﹣10,
令f(n)=﹣4n2+16n﹣10=﹣4(n﹣2)2+6,当n=1或3时,[f(n)]max=2,∴ ![]() ﹣a1≥2,解得a1≥2或a1≤﹣1.
﹣a1≥2,解得a1≥2或a1≤﹣1.
当n为偶数时,an=2n﹣3﹣a1,an+1=2n+a1,
由 ![]() ≥5成立,an+1+an=4n﹣3,可得:
≥5成立,an+1+an=4n﹣3,可得: ![]() +3a1≥﹣4n2+16n﹣12,
+3a1≥﹣4n2+16n﹣12,
令g(n)=﹣4n2+16n﹣12=﹣4(n﹣2)2+4,当n=2时,[f(n)]max=4,∴ ![]() +3a1≥4,解得a1≥1或a1≤﹣4.
+3a1≥4,解得a1≥1或a1≤﹣4.
综上所述可得:a1的取值范围是(﹣∞,﹣4]∪[2,+∞).
【解析】(1)由an+1+an=4n﹣3,n∈N* , 可得a2+a1=1,a3+a2=5,相减可得a3﹣a1=5﹣1=4,设等差数列{an}的公差为d,可得2d=4,解得d.(2)由an+1+an=4n﹣3,an+2+an+1=4n+1,可得an+2﹣an=4,a2=4.可得数列{an}的奇数项与偶数项分别成等差数列,公差都为4.对n分类讨论利用等差数列的求和公式即可得出.(3)由(2)可知:an= ![]() .当n为奇数时,an=2n﹣2+a1 , an+1=2n﹣1﹣a1 , 由
.当n为奇数时,an=2n﹣2+a1 , an+1=2n﹣1﹣a1 , 由 ![]() ≥5成立,an+1+an=4n﹣3,可得:
≥5成立,an+1+an=4n﹣3,可得: ![]() ﹣a1≥﹣4n2+16n﹣10,令f(n)=﹣4n2+16n﹣10,求出其最大值即可得出.当n为偶数时,同理可得.
﹣a1≥﹣4n2+16n﹣10,令f(n)=﹣4n2+16n﹣10,求出其最大值即可得出.当n为偶数时,同理可得.
【考点精析】通过灵活运用等差关系的确定和数列的前n项和,掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系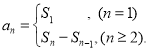 即可以解答此题.
即可以解答此题.

【题目】为大力提倡“厉行节俭,反对浪费”,某高中通过随机询问100名性别不同的学生是否做到“光盘”行动,得到如表所示联表及附表:
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算:K2= ![]() ≈3.03,参考附表,得到的正确结论是( )
≈3.03,参考附表,得到的正确结论是( )
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关”