题目内容
【题目】已知函数![]() ,若方程
,若方程![]() 有五个不同的根,则实数
有五个不同的根,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:求出f(﹣x)的解析式,根据x的范围不同得出两个不同的方程,由两个方程的关系得出f(﹣x)=f(x)在(0,+∞)上有两解,根据函数图象和导数的几何意义得出a的范围.
详解:∵f(x)=![]() ,∴f(﹣x)=
,∴f(﹣x)=![]() .
.
显然x=0是方程f(﹣x)=f(x)的一个根,
当x>0时,ex=﹣ax,①
当x<0时,e﹣x=ax,②
显然,若x0为方程①的解,则﹣x0为方程②的解,
即方程①,②含有相同个数的解,
∵方程f(﹣x)=f(x)有五个不同的根,
∴方程①在(0,+∞)上有两解,
做出y=ex(x>0)和y=﹣ax(x>0)的函数图象,如图所示:
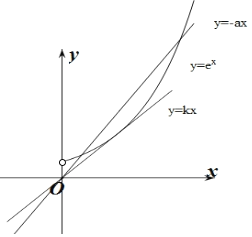
设y=kx与y=ex相切,切点为(x0,y0),
则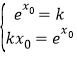 ,解得x0=1,k=e.
,解得x0=1,k=e.
∵y=ex与y=﹣ax在(0,+∞)上有两个交点,
∴﹣a>e,即a<﹣e.
故选: C.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目