题目内容
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数 ![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点![]() 代入函数
代入函数![]() 的解析式得到
的解析式得到![]() ,令
,令![]() ,由
,由![]() 可求出
可求出![]() 的值,令
的值,令![]() ,由
,由![]() 得
得![]() ,两式相减得出数列
,两式相减得出数列![]() 为等比数列,确定该数列的公比,利用等比数列的通项公式可求出数列
为等比数列,确定该数列的公比,利用等比数列的通项公式可求出数列![]() 的通项公式;
的通项公式;
(2)求出数列![]() 的通项公式,利用错位相减法求出数列
的通项公式,利用错位相减法求出数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)利用分组求和法与裂项法求出数列![]() 的前
的前![]() 项和
项和![]() ,由题意得出
,由题意得出![]()
![]() ,判断出数列
,判断出数列![]() 各项的符号,得出数列
各项的符号,得出数列![]() 的最大值为
的最大值为![]() ,利用函数
,利用函数![]() 的单调性得出该函数在区间
的单调性得出该函数在区间![]() 上的最大值为
上的最大值为![]() ,然后解不等式
,然后解不等式![]()
![]() 可得出实数
可得出实数![]() 的取值范围.
的取值范围.
(1)将点![]() 代入函数
代入函数![]() 的解析式得到
的解析式得到![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ,
,
上述两式相减得![]() ,得
,得![]() ,即
,即![]() .
.
所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,因此,
为公比的等比数列,因此,![]() ;
;
(2)![]() ,
,![]() ,
,
因此![]() ,①
,①
![]() ,②
,②
由①![]() ②得
②得![]()
![]() ,
,
所以![]() ;
;
(3)![]() .
.
令![]() 为
为![]() 的前
的前![]() 项和,
项和,
则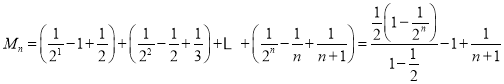
![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,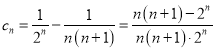 ,
,
令![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,此时,数列
,此时,数列![]() 为单调递减数列,
为单调递减数列,![]() ,
,
则![]() ,即
,即![]() ,
,
那么当![]() 时,数列
时,数列![]() 为单调递减数列,此时
为单调递减数列,此时![]() ,则
,则![]() .
.
因此,数列![]() 的最大值为
的最大值为![]() .
.
又![]() ,函数
,函数![]() 单调递增,
单调递增,
此时,函数![]() 的最大值为
的最大值为![]() .
.
因为对任意的![]() ,存在
,存在![]() ,
,![]() .
.
所以![]() ,解得
,解得![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() .
.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
表中![]() ,
,![]() .
.
为了预测印刷20千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中选择的模型,求![]() 关于
关于![]() 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
