题目内容
12.已知顶点为坐标原点O的抛物线C1与双曲线C2:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)都过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且它们有共同的一个焦点F.则双曲线C2的离心率是( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 设抛物线方程为y2=2px(p>0),将M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$)代入,可求抛物线方程,再利用双曲线的定义可求双曲线的a,再由离心率公式可得e.
解答 解:设抛物线方程为y2=2px(p>0),
将M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$)代入y2=2px,得p=2.
∴抛物线方程为y2=4x,焦点为F(1,0),
由题意知双曲线的焦点为F1(-1,0),F2(1,0),∴c=1,
对于双曲线,2a=|MF1|-|MF2|=$\sqrt{(\frac{2}{3}+1)^{2}+(\frac{2\sqrt{6}}{3})^{2}}$-$\sqrt{(\frac{2}{3}-1)^{2}+(\frac{2\sqrt{6}}{3})^{2}}$=$\frac{7}{3}$-$\frac{5}{3}$=$\frac{2}{3}$,
∴a=$\frac{1}{3}$,
∴e=$\frac{c}{a}$=3.
故选B.
点评 本题主要考查利用待定系数法求抛物线、双曲线方程,注意挖掘题目隐含,将问题等价转化.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
3.已知实数ai,bi(i=1,2,3)满足a1<a2<a3,b1<b2<b3,且(ai-b1)(ai-b2)(ai-b3)=-1(i=1,2,3),则下列结论正确的是( )
| A. | b1<a1<a2<b2<b3<a3 | B. | a1<b1<b2<a2<a3<b3 | ||
| C. | a1<a2<b1<b2<a3<b3 | D. | b1<b2<a1<a2<b3<a3 |
7. 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )| A. | 16$\sqrt{2}$+16π | B. | 16$\sqrt{2}$+8π | C. | 8$\sqrt{2}$+8π | D. | 8$\sqrt{2}$+16π |
17.如图,在正方体ABCD-A1B1C1D1中,下面结论不正确的是( )
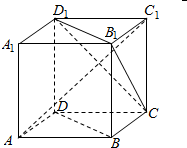

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
 如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△ECD都是边长为2的正三角形,平面ECD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$. 已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).
已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).