��Ŀ����
5�� ��֪����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{1}{2}$���̰��᳤Ϊ$\sqrt{3}$��б��Ϊ$\frac{b}{a}$�Ķ�ֱ��l����ԲC����A��B���㣬��x�ᣬy���ཻ��P��Q���㣨��ͼ��ʾ����
��֪����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{1}{2}$���̰��᳤Ϊ$\sqrt{3}$��б��Ϊ$\frac{b}{a}$�Ķ�ֱ��l����ԲC����A��B���㣬��x�ᣬy���ཻ��P��Q���㣨��ͼ��ʾ������������ԲC�ı����̣�
������̽��$\frac{|AP|}{|BQ|}$�Ƿ�Ϊ��ֵ�����Ƕ�ֵ��������ö�ֵ�������Ƕ�ֵ����˵�����ɣ�
���� ���������⣬��b=$\sqrt{3}$������a2-c2=3����$e=\frac{c}{a}=\frac{1}{2}$���ã�a=2c�����Բ���̣�
������ֱ��l�ķ���Ϊ��y=$\frac{\sqrt{3}}{2}x+n$������������$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{2}x+n}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$�������е㹫ʽ�������֤�����ۣ�
��� �⣺���������⣬��b=$\sqrt{3}$������a2-c2=3���٣�
��$e=\frac{c}{a}=\frac{1}{2}$���ã�a=2c����
�ɢ٢ڵ�a=2��������ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
���ٵ�ֱ��l��ԭ��ʱ������Բ�öԳ��ԣ���֪��|AP|=|BQ|����$\frac{|AP|}{|BQ|}=1$
���¸�������֤�����̣�
�ɣ���$\frac{b}{a}=\frac{\sqrt{3}}{2}$������ֱ��l�ķ���Ϊ��y=$\frac{\sqrt{3}}{2}x+n$
��y=0����x=$-\frac{2\sqrt{3}}{3}n$����P��$-\frac{2\sqrt{3}}{3}n��0$����
��x=0����y=n����Q��0��n��
��PQ�е������Ϊ$-\frac{\sqrt{3}}{3}n$
����������$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{2}x+n}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$
��ȥy����3x2+2$\sqrt{3}$nx+2n2-6=0
���=12n2-12��2n2-6����0����$-\sqrt{6}��n��\sqrt{6}$
��$-\sqrt{6}��n��\sqrt{6}$ʱ��ֱ��l����ԲC�ཻ��A��B
��A��x1��y1����B��x2��y2��
��${x}_{1}+{x}_{2}=-\frac{2\sqrt{3}}{3}n$��$\frac{{x}_{1}+{x}_{2}}{2}=-\frac{\sqrt{3}}{3}n$
�����߶�AB���е������Ϊ$-\frac{\sqrt{3}}{3}n$
����Ϊ�߶�PQ���е�ĺ�����Ϊ$-\frac{\sqrt{3}}{3}n$
����$\frac{|AP|}{|BQ|}=1$
�ۺϢ٢ڿ�֪��$\frac{|AP|}{|BQ|}$Ϊ��ֵ���Ҷ�ֵΪ1
���� ������Ҫ����ֱ����Բ���ߵ��ۺ����⣬�����⣮�ڸ߿��г���Ϊѹ����Ŀ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�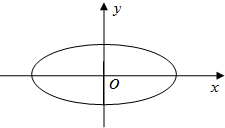 ��ͼ��������ԭ�����Բ�Ľ�����x���ϣ����᳤Ϊ4������Ϊ2$\sqrt{3}$��OΪ����ԭ�㣮
��ͼ��������ԭ�����Բ�Ľ�����x���ϣ����᳤Ϊ4������Ϊ2$\sqrt{3}$��OΪ����ԭ�㣮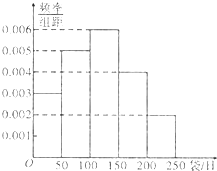 ��ͼ��ʾ����ijĸӤ��Ʒר����������������̷۵����ۼ�¼���Ƶ�����������Ƶ�ʷֲ�ֱ��ͼ��������������������Ƶ����Ϊ���ʣ�������ÿ����������������
��ͼ��ʾ����ijĸӤ��Ʒר����������������̷۵����ۼ�¼���Ƶ�����������Ƶ�ʷֲ�ֱ��ͼ��������������������Ƶ����Ϊ���ʣ�������ÿ����������������