题目内容
已知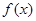 定义域为R,满足:①
定义域为R,满足:①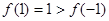 ;
;
②对任意实数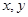 ,有
,有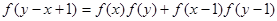 .
.
(Ⅰ)求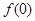 ,
,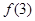 的值;
的值;
(Ⅱ)判断函数的奇偶性与周期性,并求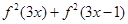 的值;
的值;
(Ⅲ)是否存在常数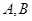 ,使得不等式
,使得不等式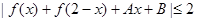 对一切实数
对一切实数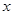 成立.如果存在,求出常数
成立.如果存在,求出常数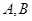 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
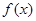 定义域为R,满足:①
定义域为R,满足:①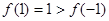 ;
;②对任意实数
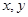 ,有
,有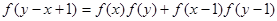 .
.(Ⅰ)求
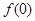 ,
,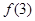 的值;
的值;(Ⅱ)判断函数的奇偶性与周期性,并求
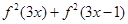 的值;
的值;(Ⅲ)是否存在常数
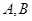 ,使得不等式
,使得不等式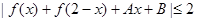 对一切实数
对一切实数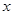 成立.如果存在,求出常数
成立.如果存在,求出常数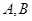 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.解:(Ⅰ)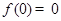 .
. 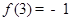 .
.
(Ⅱ)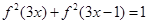 .
.
(Ⅲ)存在常数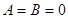 ,使得不等式
,使得不等式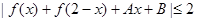 对一切实数
对一切实数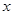 成立,且
成立,且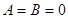 为满足题设的唯一一组值.
为满足题设的唯一一组值.
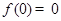 .
. 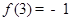 .
.(Ⅱ)
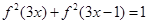 .
.(Ⅲ)存在常数
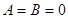 ,使得不等式
,使得不等式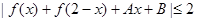 对一切实数
对一切实数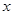 成立,且
成立,且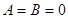 为满足题设的唯一一组值.
为满足题设的唯一一组值. 本试题主要是考查了抽象函数赋值思想的运用。
(1)对于x,y适当的赋值,求解得到f(0),f(3)的值
(2)在条件中令x=0,那么得到函数的周期为4,然后结合定义证明其奇偶性。并求解函数值。
(3)运用函数的周期性和函数与不等式的关系进行求解运算即可。
(1)对于x,y适当的赋值,求解得到f(0),f(3)的值
(2)在条件中令x=0,那么得到函数的周期为4,然后结合定义证明其奇偶性。并求解函数值。
(3)运用函数的周期性和函数与不等式的关系进行求解运算即可。

练习册系列答案
相关题目
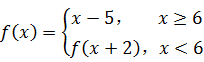 ,则
,则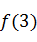 等于( )
等于( )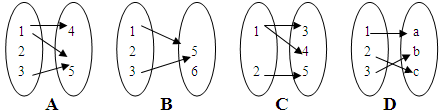
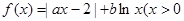 ,实数a,b为常数),
,实数a,b为常数),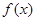 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;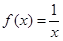 在(0,1]上解的个数
在(0,1]上解的个数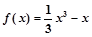 在
在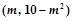 上有最小值,则实数m的取值范围是 .
上有最小值,则实数m的取值范围是 .
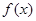 在
在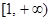 上为增函数,求正实数
上为增函数,求正实数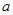 的取值范围;
的取值范围; ,求证:
,求证: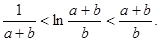
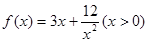 的最小值为_____________
的最小值为_____________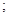
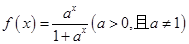 ,若用
,若用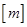 表示不超过实数
表示不超过实数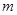 的最大整数,则函数
的最大整数,则函数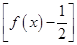
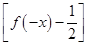 的值域为_____________.
的值域为_____________. 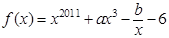 ,
,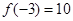 ,则
,则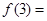 ______________.
______________.