题目内容
若函数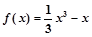
在
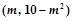上有最小值，则实数m的取值范围是 .
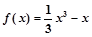在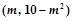上有最小值，则实数m的取值范围是 .
因为
在给定区间上
，有最小值，利用导数，确定单调区间，进而分析极值，进而得到最值，那么实数m的取值范围是【-2,1】。
在给定区间上，有最小值，利用导数，确定单调区间，进而分析极值，进而得到最值，那么实数m的取值范围是【-2,1】。
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
.给出函数
下列性质：①函数的定义域和值域均为
；②函数的图像关于原点成中心对称；③函数在定义域上单调递增；④
（其中
为函数的定义域）；⑤
为函数
。请写出所有关于函数
的图象是曲线C，直线
与曲线
的解析式；
上的最大值和最小值.
定义域为R，满足：①
；
，有
.
，
的值；
的值；
，使得不等式
对一切实数
成立.如果存在，求出常数
时，
则f (－1)＝ .
（
）的最大值为1，对任意
，有
。
的解析式；
，其中
，求
的值。
的定义域为
，若存在非零实数
使得对于任意
，有
，且
，则称
上的
的函数
时，
，且
的取值范围是 
.
，则
______
每日10分钟口算心算速算天天练系列答案题目内容
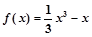在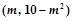上有最小值，则实数m的取值范围是 .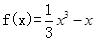在给定区间上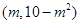，有最小值，利用导数，确定单调区间，进而分析极值，进而得到最值，那么实数m的取值范围是【-2,1】。每日10分钟口算心算速算天天练系列答案