Question

【题目】在中，三内角A,B,C的对边分别为a,b,c.

（1）若，求；

（2）若，且为钝角，证明： ，并求的取值范围.

Answer 1

【答案】（1），（2）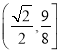

【解析】试题分析：

(1)由题意结合正弦定理可得或，结合两角和差正余弦公式可得；

(2)利用题意得到关于sinA的二次函数，结合二次函数的性质可得的取值范围是.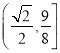

试题解析：

(1)由正弦定理可得，

∵c,A=45°，a=2，

∴sinC=，

∴C=60°或120°，

由正弦定理可得

当C=60°,sinB=sin(A+C)=sin45°cos60°+cos45°sin60°=

∴b=，

当C=120°,sinB=sin(A+C)=sin45°cos120°+cos45°sin120°=

∴b=，

(2)由题意得a=btanA，

∴由正弦定理得，则sinB=cosA，

∵B为钝角,∴，

∴BA=；

∴C=π(A+B)=π(A++A)= 2A>0，

∴A∈(0, )，

∴sinA+sinC=sinA+sin(2A)=sinA+cos2A=sinA+12sin/span>2A=2(sinA)2+，

∵A∈(0, ),∴0<sinA<，

∴由二次函数可知, ，

∴sinA+sinC的取值范围为.