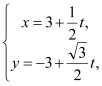题目内容
【题目】已知点![]() ,
,![]() 是函数
是函数![]()
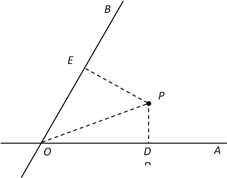
![]() 图象上的任意两点,且角
图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的 最小值为
的 最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用三角函数的定义求出![]() 的值,由
的值,由![]() 时,
时,![]() 的最小值为
的最小值为![]() ,可得函数的周期,从而可求
,可得函数的周期,从而可求![]() ,进而可求函数
,进而可求函数![]() 的解析式;(2)当
的解析式;(2)当![]() 时,不等式
时,不等式![]() 恒成立,等价于
恒成立,等价于![]() ,先求出得
,先求出得![]() 的最大值,由此可得
的最大值,由此可得![]() 的取值范围.
的取值范围.
试题解析:(1)角![]() 的终边经过点
的终边经过点![]() ,
,![]() ,
,
![]() ,
,![]() .
.
由![]() 时,
时,![]() 的最小值为
的最小值为![]() ,得
,得![]() ,即
,即![]() ,
,
![]() ∴
∴![]()
(2)当![]() 时,
时,![]() , 于是,
, 于是,![]() ,
,![]()
等价于![]()
由 ![]() , 得
, 得![]() 的最大值为
的最大值为![]()
所以,实数![]() 的取值范围是
的取值范围是![]()
注:用别的方法求得![]() ,只要正确就给3分.
,只要正确就给3分.
【方法点晴】本题主要考查三角函数图像与性质及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的范围的.
的范围的.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
【题目】为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩,成绩如下表:
甲单位 | 87 | 88 | 91 | 91 | 93 |
乙单位 | 85 | 89 | 91 | 92 | 93 |
(1)根据表中的数据,分别求出甲、乙两单位职工成绩的平均数和方差,并判断哪个单位对法律知识的掌握更稳定;
(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.