题目内容
8.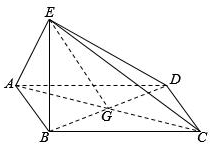 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(Ⅰ)证明:平面AEC⊥平面BED;
(Ⅱ)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为$\frac{\sqrt{6}}{3}$,求该三棱锥的侧面积.
分析 (Ⅰ)根据面面垂直的判定定理即可证明:平面AEC⊥平面BED;
(Ⅱ)根据三棱锥的条件公式,进行计算即可.
解答 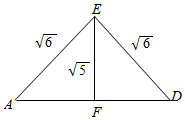 证明:(Ⅰ)∵四边形ABCD为菱形,
证明:(Ⅰ)∵四边形ABCD为菱形,
∴AC⊥BD,
∵BE⊥平面ABCD,
∴AC⊥BE,
则AC⊥平面BED,
∵AC?平面AEC,
∴平面AEC⊥平面BED;
解:(Ⅱ)设AB=x,在菱形ABCD中,由∠ABC=120°,得AG=GC=$\frac{\sqrt{3}}{2}$x,GB=GD=$\frac{x}{2}$,
∵AE⊥EC,△EBG为直角三角形,
∴EG=$\frac{1}{2}$AC=AG=$\frac{\sqrt{3}}{2}$x,
则BE=$\sqrt{E{G}^{2}-B{G}^{2}}$=$\frac{\sqrt{2}}{2}$x,
∵三棱锥E-ACD的体积V=$\frac{1}{3}×\frac{1}{2}AC•GD•BE$=$\frac{\sqrt{6}}{24}{x}^{3}$=$\frac{\sqrt{6}}{3}$,
解得x=2,即AB=2,
∵∠ABC=120°,
∴AC2=AB2+BC2-2AB•BCcosABC=4+4-2×$2×2×(-\frac{1}{2})$=12,
即AC=$\sqrt{12}=2\sqrt{3}$,
在三个直角三角形EBA,EBG,EBC中,斜边AE=EC=ED,
∵AE⊥EC,∴△EAC为等腰三角形,
则AE2+EC2=AC2=12,
即2AE2=12,
∴AE2=6,
则AE=$\sqrt{6}$,
∴从而得AE=EC=ED=$\sqrt{6}$,
∴△EAC的面积S=$\frac{1}{2}×EA•EC=\frac{1}{2}×\sqrt{6}×\sqrt{6}$=3,
在等腰三角形EAD中,过E作EF⊥AD于F,
则AE=$\sqrt{6}$,AF=$\frac{1}{2}AD$=$\frac{1}{2}×2=1$,
则EF=$\sqrt{(\sqrt{6})^{2}-{1}^{2}}=\sqrt{5}$,
∴△EAD的面积和△ECD的面积均为S=$\frac{1}{2}×2×\sqrt{5}$=$\sqrt{5}$,
故该三棱锥的侧面积为3+2$\sqrt{5}$.
点评 本题主要考查面面垂直的判定,以及三棱锥体积的计算,要求熟练掌握相应的判定定理以及体积公式.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
| A. | 8cm3 | B. | 12cm3 | C. | $\frac{32}{3}c{m^3}$ | D. | $\frac{40}{3}c{m^3}$ |
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率是$\frac{\sqrt{2}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2$\sqrt{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率是$\frac{\sqrt{2}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2$\sqrt{2}$. 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.