Question

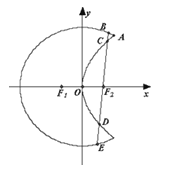
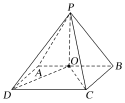
【题目】如图，在四棱锥P－ABCD中，侧面PAB⊥底面ABCD，底面ABCD为矩形，PA＝PB，O为AB的中点，OD⊥PC.

(Ⅰ) 求证：OC⊥PD；

（II）若PD与平面PAB所成的角为30°，求二面角D－PC－B的余弦值.

Answer 1

【答案】(I)详见解析(II)

【解析】

（Ⅰ）连结OP，推导出OP⊥AB，从而OP⊥平面ABCD，由OP⊥OD，OP⊥OC，得OD⊥OC，再由OP⊥OC，能证明OC⊥PD．

（Ⅱ）取CD的中点E，以O为原点，OE，OB，OP所在的直线分别为x，y，z轴建立空间直角坐标系O－xyz.求出平面DPC与平面BPC的法向量，由此能求出二面角D﹣PC﹣B的余弦值．

(I)证明　如图，连接OP.

∵PA＝PB，O为AB的中点，

∴OP⊥AB.

∵侧面PAB⊥底面ABCD，

∴OP⊥平面ABCD，

∴OP⊥OD，OP⊥OC.

∵OD⊥PC，∴OD⊥平面OPC，

∴OD⊥OC，

又OP⊥OC，OP∩OD＝O，

∴OC⊥平面OPD，

∴OC⊥PD.

(II)解:法一　取CD的中点E，以O为原点，OE，OB，OP所在的直线分别为x，y，z轴建立空间直角坐标系O－xyz.在矩形ABCD中，由(1)得OD⊥OC，∴AB＝2AD，不妨设AD＝1，则AB＝2.

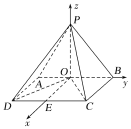
∵侧面PAB⊥底面ABCD，底面ABCD为矩形，

∴DA⊥平面PAB，CB⊥平面PAB，△DPA≌△CPB，

∴∠DPA为直线PD与平面PAB所成的角，

∴∠DPA＝30°，∠CPB＝30°，PA＝PB＝，

∴B(0，1，0)，C(1，1，0)，D(1，－1，0)，P(0，0，)，从而＝(1，1，－)，＝(0，－2，0).

设平面PCD的法向量为n1＝(x1，y1，z1)，

由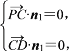得可取n1＝(，0，1).

同理，可取平面PCB的一个法向量为n2＝(0，－，－1).

于是cos〈n1，n2〉＝＝－，

∴二面角D－PC－B的余弦值为－.

法二　在矩形ABCD中，由(1)得OD⊥OC，∴AB＝2AD，不妨设AD＝1，则AB＝2.

∵侧面PAB⊥底面ABCD，底面ABCD为矩形，

∴DA⊥平面PAB，CB⊥平面PAB，△DPA≌△CPB，

∴∠DPA为直线PD与平面PAB所成的角，

∴∠DPA＝30°，∠CPB＝30°，PA＝PB＝，

∴DP＝CP＝2，

∴△PDC为等边三角形.

设PC的中点为M，连接DM，则DM⊥PC.

在Rt△CBP中，过M作NM⊥PC，交PB于点N，连接ND，则∠DMN为二面角D－PC－B的一个平面角.

由于∠CPB＝30°，PM＝1，故在Rt△PMN中，MN＝，PN＝.

∵cos∠APB＝＝，

∴AN2＝＋3－2×××＝3，

∴ND2＝3＋1＝4，

∴cos∠DMN＝＝－，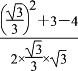

即二面角D－PC－B的余弦值为－.