题目内容
【题目】某农场有一块等腰直角三角形的空地![]() ,其中斜边
,其中斜边![]() 的长度为400米.为迎接“五一”观光游,欲在边界
的长度为400米.为迎接“五一”观光游,欲在边界![]() 上选择一点
上选择一点![]() ,修建观赏小径
,修建观赏小径![]() ,其中
,其中![]() 分别在边界
分别在边界![]() 上,小径
上,小径![]() 与边界
与边界![]() 的夹角都为
的夹角都为![]() .区域
.区域![]() 和区域
和区域![]() 内种植郁金香,区域
内种植郁金香,区域![]() 内种植月季花.
内种植月季花.

(1)探究:观赏小径![]() 与
与![]() 的长度之和是否为定值?请说明理由;
的长度之和是否为定值?请说明理由;
(2)为深度体验观赏,准备在月季花区域内修建小径![]() ,当
,当![]() 点在何处时,三条小径
点在何处时,三条小径![]() 的长度和最小?
的长度和最小?
【答案】(1)为定值,理由见解析;(2)![]() 是
是![]() 的中点.
的中点.
【解析】
(1)根据题意可得![]() ,结合正弦定理可分别用
,结合正弦定理可分别用![]() 表示出
表示出![]() 与
与![]() ,即可确定
,即可确定![]() 是否为定值;
是否为定值;
(2)在![]() 中,由余弦定理可表示出
中,由余弦定理可表示出![]() ,结合基本不等式即可得
,结合基本不等式即可得![]() ,根据(1)中
,根据(1)中![]() 为定值,即可知不等式取等号的条件,进而确定
为定值,即可知不等式取等号的条件,进而确定![]() 点的位置及三条小径的长度和.
点的位置及三条小径的长度和.
(1)![]() 为等腰直角三角形,小径
为等腰直角三角形,小径![]() 与边界
与边界![]() 的夹角都为
的夹角都为![]() ,
,
在![]() 中,所以
中,所以![]() ,
,
故由正弦定理可得![]() ,
,
即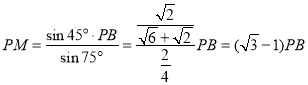 .
.
同理![]() .
.
故![]()
![]() 为定值.
为定值.
(2)在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
即![]() ,
,
所以![]() ,
,![]() .
.
又由(1)有![]() ,
,
故![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
故当![]() 点
点![]() 的中点位置时,三条小径
的中点位置时,三条小径![]() 的长度和最小为
的长度和最小为![]() .
.

练习册系列答案
相关题目
【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 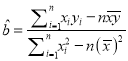 ,
, ![]() .
.


