题目内容
【题目】设椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于点
交于点![]() ,
,![]() . 若
. 若![]() ,且
,且![]() ,则
,则![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
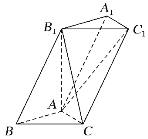
由题意画出图形,由|PF2|=|F1F2|,3|PF1|=4|QF1|,利用椭圆的定义可得:|PF1|=2a﹣2c,进一步求出|QF1|,|QF2|,在等腰△PF1F2中,求得得cos∠PF1F2.在△QF1F2中,由余弦定理可得cos∠QF1F2,利用cos∠PF1F2+cos∠QF1F2=0,化简求得5a=7c,两边平方后结合隐含条件求得![]() 的值,则C的离心率可求.
的值,则C的离心率可求.
如图所示,
∵|PF2|=|F1F2|,
∴|PF2|=2c,则|PF1|=2a﹣2c.
∵3|PF1|=4|QF1|,
∴|QF1|![]() (2a﹣2c)
(2a﹣2c)![]() (a﹣c),
(a﹣c),
则|QF2|=2a![]() (a﹣c)
(a﹣c)![]() c.
c.
在等腰△PF1F2中,可得cos∠PF1F2![]() .
.
在△QF1F2中,由余弦定理可得: ,
,
由cos∠PF1F2+cos∠QF1F2=0,得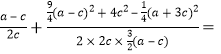 0,
0,
整理得:![]() ,∴5a=7c,
,∴5a=7c,
则25a2=49c2=49(a2﹣b2),
∴![]() .
.
则![]() .
.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目